- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:30.
- Sist endret 2025-01-23 12:42.
Det er mange forskjellige former for flate former, og det er mange grunner til at du kanskje vil beregne areal: fra å gjøre lekser til å anslå hvor mye maling som trengs for å male om en stue. Ikke bekymre deg, wikiHow har svaret! Start fra trinn 1 nedenfor for å vite hvordan du beregner arealet til et flyfigur.
Steg
Metode 1 av 7: Firkant, rektangel og parallellogram
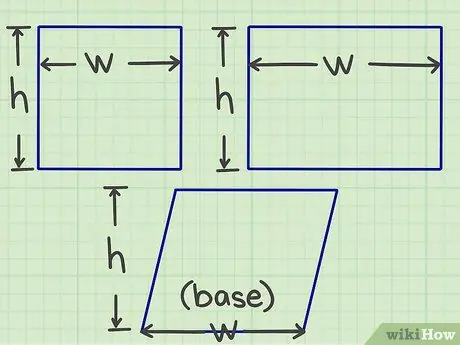
Trinn 1. Mål lengde og bredde
Begynn å måle eller finne ut lengden og bredden på den flate formen (eller med andre ord størrelsen på hver av de to sidene som møtes på et tidspunkt).
- For et parallellogram må du finne basen og høyden, men i enkle termer er ideen den samme som lengde og bredde.
- I den virkelige verden må du kanskje måle det selv, men når det gjelder lekser, har læreren vanligvis allerede skrevet ned tallene sammen med et bilde av formen.
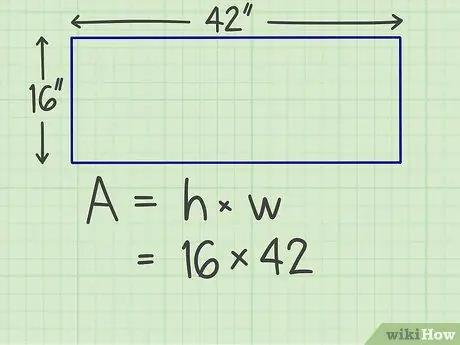
Trinn 2. Multipliser sidene
Multipliser den ene siden med den andre. Anta for eksempel at du har et rektangel med en bredde på 16 tommer og en lengde på 42 tommer, så du må beregne 16 x 42.
Hvis du beregner arealet til en firkant (tidligere en firkant), kan du spare tid ved å kvadrere en av sidene ved hjelp av en kalkulator. Hvis siden måler 4 m, trykker du på 4 -tasten og deretter på firkanttasten på kalkulatoren for å vise resultatet. Kvadrat betyr å multiplisere et tall med seg selv
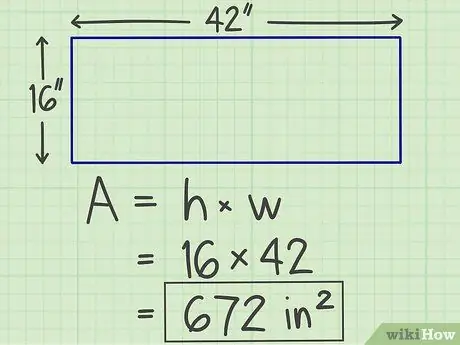
Trinn 3. Skriv ned resultatene
Multiplikasjonen du gjorde tidligere vil produsere et tall, som er arealet til planet du beregner, med enheten "kvadrat". Dermed har rektangelet vi beregnet tidligere et areal på 672 kvadratmeter.
Noen ganger er denne kvadratiske enheten også skrevet som en liten 2 som stiger litt etter enhetsnavnet (som skrivekrefter)
Metode 2 av 7: Trapes
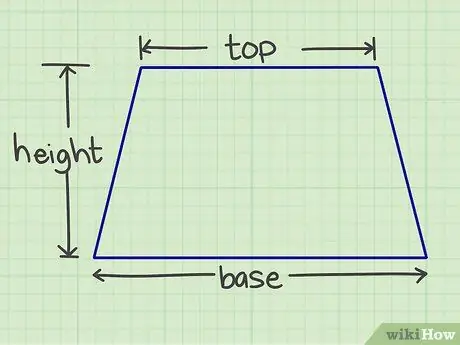
Trinn 1. Mål det nødvendige tallet
Du må måle sokkelen, taket og høyden. Basen og taket er parallelle sider, mens høyden er en vinkelrett linje som forbinder de to parallelle sidene.
I den virkelige verden må du kanskje måle det selv, men når det gjelder lekser, har læreren vanligvis allerede skrevet ned tallene sammen med et bilde av formen
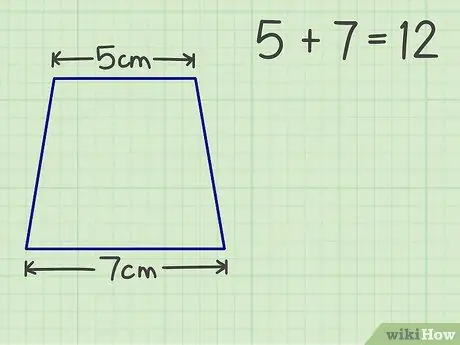
Trinn 2. Legg sammen de to parallelle sidene
For eksempel har vår trapez et tak på 5 cm og en base på 7 cm. Summen av de to parallelle sidene er 12.
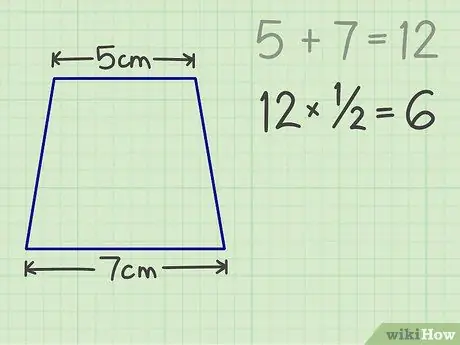
Trinn 3. Multipliser tallet med 1/2, resultatet er 6
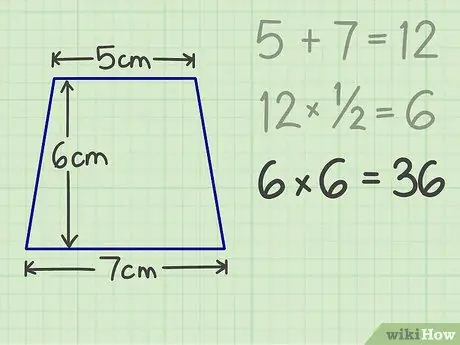
Trinn 4. Etter det multipliserer du resultatet med høyden
For eksempel, hvis en trapes har en høyde på 6 cm, er det endelige resultatet 36.
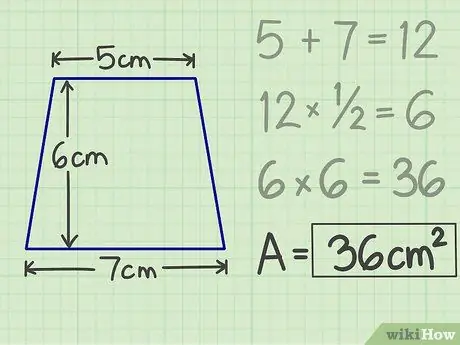
Trinn 5. Skriv ned resultatene
Multiplikasjonen du gjorde tidligere vil produsere et tall, nemlig området til trapes. Så for en trapes med et tak på 5 cm, en base på 7 cm og en høyde på 6 cm, er området 36 cm kvadratisk.
Metode 3 av 7: Sirkel
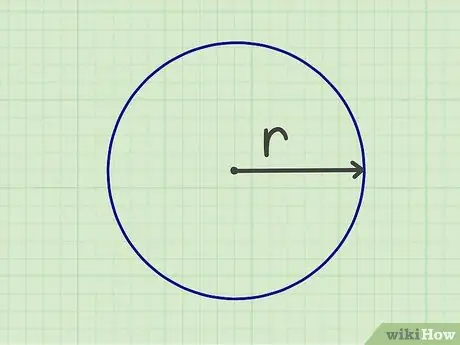
Trinn 1. Mål radius
For å kunne beregne arealet til en sirkel, må du måle radius. radius er avstanden fra midten av sirkelen til kanten. Du kan også måle radius ved å måle diameteren (bredden på sirkelen fra kant til kant), og deretter dele tallet med to.
I den virkelige verden må du kanskje måle det selv, men når det gjelder lekser, har læreren vanligvis allerede skrevet ned tallene sammen med et bilde av formen
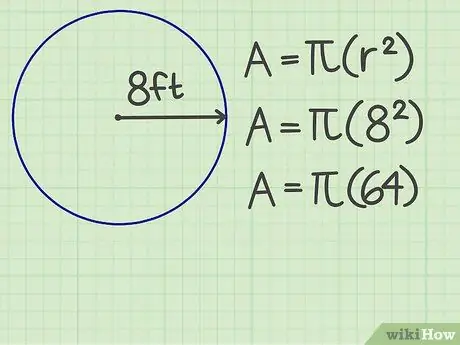
Trinn 2. Firkant fingrene
Multipliser antallet radier av seg selv. For eksempel er radiusen til en sirkel 8 fot, så resultatet er 64.
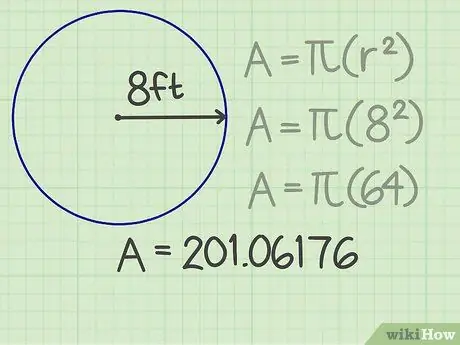
Trinn 3. Multipliser resultatet med pi
Pi (π) er et viktig tall som brukes i forskjellige formler. Hvis du bruker en kalkulator, trykker du på pi -tasten for å få virkelig nøyaktige resultater. For å gjøre beregningene dine enklere, kan du avrunde pi til noen få sifre etter kommaet, for eksempel 3, 14159. Når du multipliserer dette tallet med kvadratet i radius, er resultatet 201, 06176.
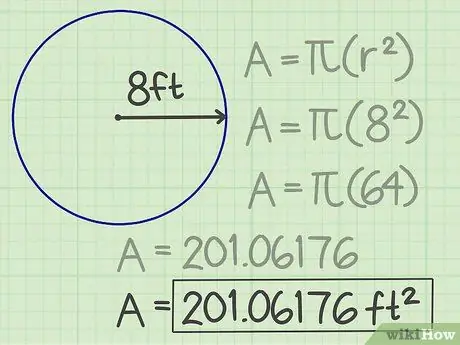
Trinn 4. Skriv ned resultatene
Tallet oppnådd, 201, 06176 er arealet av sirkelen. Dermed er arealet 201 06176 kvadratmeter.
Metode 4 av 7: Sektor (Juring)
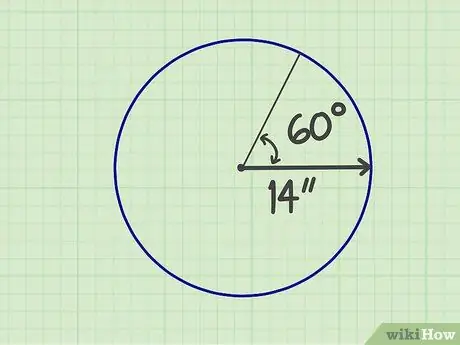
Trinn 1. Mål de nødvendige tallene
En sektor er et snitt av en sirkel dannet av to radier og en kant, slik at formen er som en vifte. Du må vite størrelsen på radiusen og vinkelen som utgjør "viften". Anta for eksempel at en sektor har en radius på 14 tommer og en vinkel på 60 grader.
I den virkelige verden må du kanskje måle det selv, men når det gjelder lekser, har læreren vanligvis allerede skrevet ned tallene sammen med et bilde av formen
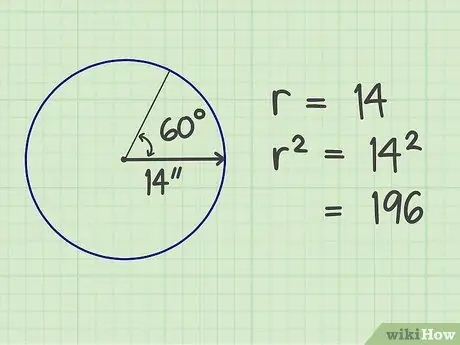
Trinn 2. Firkant fingrene
Multipliser antallet radier av seg selv. Resultatet er 196 (14x14).

Trinn 3. Multipliser resultatet med pi
Pi (π) er et viktig tall som brukes i forskjellige formler. Hvis du bruker en kalkulator, trykker du på pi -tasten for å få virkelig nøyaktige resultater. Ellers, for å gjøre beregningene enklere, kan du avrunde pi til noen få sifre etter kommaet, for eksempel 3, 14159. Hvis du multipliserer dette tallet med kvadratet i radius, er resultatet 615, 75164.

Trinn 4. Del målingen av vinkelen med 360
Del sektorviftevinkelen med 360 (målet på en hel sirkelvinkel). For eksemplet ovenfor er resultatet rundt 0,166. Hvis du beregner det med en kalkulator, er resultatet faktisk lengre og iterativt, men her er det avrundet for å gjøre beregningen enklere.

Trinn 5. Multipliser dette tallet med det forrige nummeret
Multipliser tallet du får etter at du har delt vinkelen med 360, med tallet du fikk tidligere etter å ha multiplisert pi med kvadratet i radius. for eksemplet ovenfor er resultatet 102, 214 (etter avrunding).
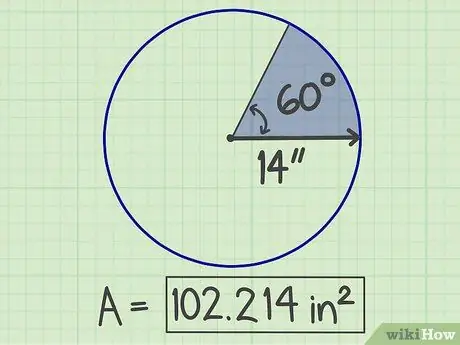
Trinn 6. Skriv ned resultatene
Tallet som er oppnådd er området i sektoren, som er 102, 214 kvadratmeter.
Metode 5 av 7: Ellipse
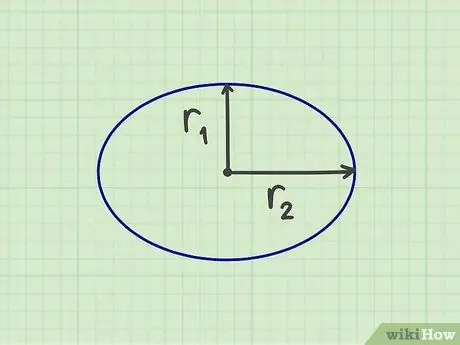
Trinn 1. Mål det nødvendige tallet
For å beregne arealet til en ellipse må du måle to "radier", nemlig den korte radiusen og den lange radiusen, som er halv bredde og halv høyde på ellipsen. Du kan også måle den korte radiusen fra midten av ellipsen til den korteste siden, og den lange radiusen fra midten av ellipsen til den lengste siden. Den korte radiusen skal danne en rett vinkel mot den lange radiusen.
I den virkelige verden må du kanskje måle det selv, men når det gjelder lekser, har læreren vanligvis allerede skrevet ned tallene sammen med et bilde av formen
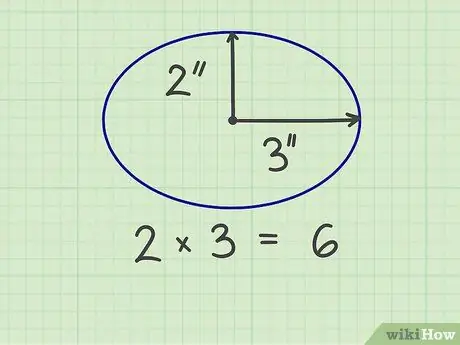
Trinn 2. Multipliser de to fingrene
For eksempel er en ellipse 6 tommer bred og 4 tommer høy, så radiene er 3 tommer og 2 tommer. Når de to tallene multipliseres, er resultatet 6 (3 x 2).

Trinn 3. Multipliser resultatet med pi
Pi (π) er et viktig tall som brukes i forskjellige formler. Hvis du bruker en kalkulator, trykker du på pi -tasten for å få virkelig nøyaktige resultater. Ellers, for å gjøre beregningene enklere, kan du avrunde pi til et par sifre etter kommaet, for eksempel 3, 14159. Når du ganger dette tallet med kvadratet i radius, er resultatet 18, 84954.
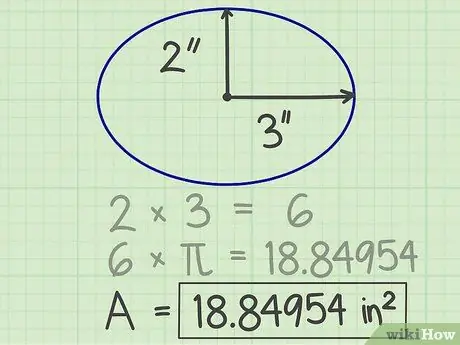
Trinn 4. Skriv ned resultatene
Tallet oppnådd fra beregningen ovenfor er ellipsens areal. I eksemplet ovenfor er ellipsens areal 18,84954 kvadratmeter.
Metode 6 av 7: Triangle
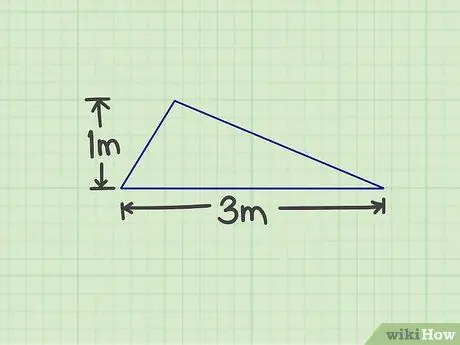
Trinn 1. Mål det nødvendige tallet
Du må måle basisen og høyden på trekanten. Enhver side av trekanten kan være basen, så lenge du kan måle høyden. For eksempel er det en trekant med en base på 3 m og en høyde på 1 m.
I den virkelige verden må du kanskje måle det selv, men når det gjelder lekser, har læreren vanligvis allerede skrevet ned tallene sammen med et bilde av formen
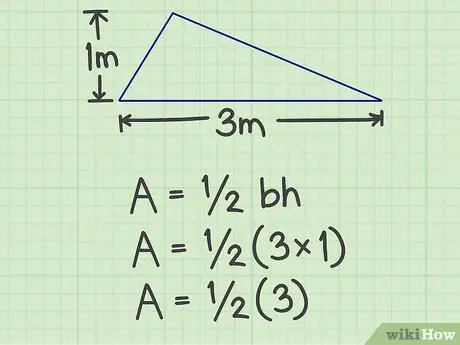
Trinn 2. Multipliser basen med høyden
For eksemplet ovenfor er resultatet 3 (3x1).
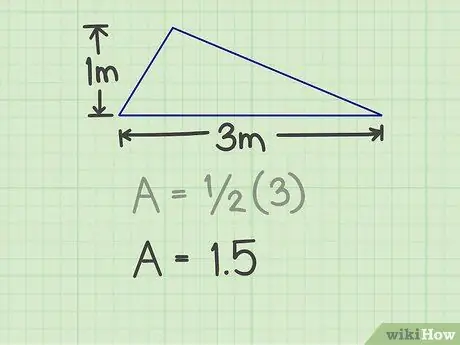
Trinn 3. Multipliser resultatet med 1/2
Denne multiplikasjonen vil gi tallene 1, 5.
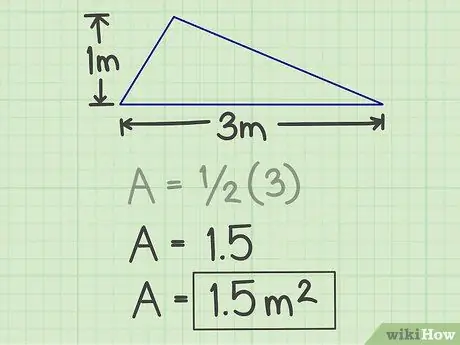
Trinn 4. Skriv ned resultatene
Tallet generert av beregningen ovenfor er arealet av trekanten, og med eksemplet ovenfor er området 1,5 kvadratmeter.
Metode 7 av 7: Kompleks flatbygning
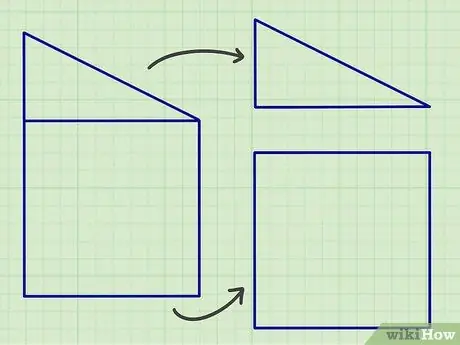
Trinn 1. Del komplekse planformer i deler som består av de geometriske standardformene ovenfor
Hvis det du gjør er lekser, kan det være lett å dele den komplekse formen i de flate formene som ble diskutert tidligere, men i den virkelige verden må du kanskje dele den flate formen i mange flate former for å få et nøyaktig beregningsresultat.
En god måte å starte er å lete etter linjer som er parallelle eller som danner en viss vinkel, siden de fleste flate former består av disse formene
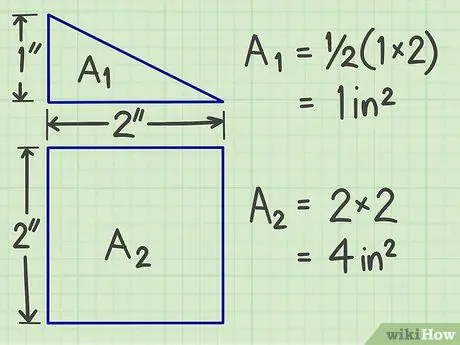
Trinn 2. Beregn arealet for hver av flyfigurene som følge av separasjonen
Bruk metodene ovenfor for å få området til hver flat form.
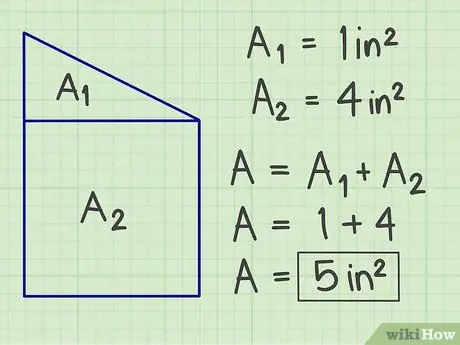
Trinn 3. Legg sammen resultatene
Legg sammen alle de beregnede områdene for å få det totale arealet til din komplekse planfigur.
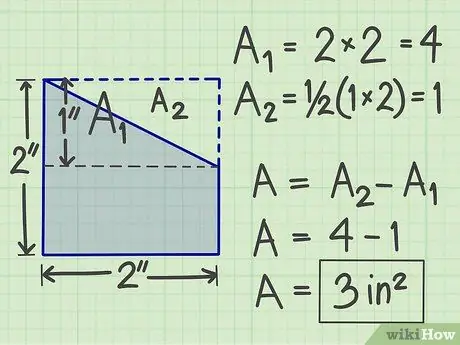
Trinn 4. Bruk en annen metode
Det er mange andre måter du kan prøve, avhengig av formen på den komplekse flate formen. For eksempel kan du også legge til en imaginær planform slik at den blir en standard geometrisk planform. Deretter beregner du området, og trekker deretter området til den imaginære flate formen du pleide å legge til.
Tips
- Bruk denne kalkulatoren hvis du trenger hjelp til å løse matematiske beregninger.
- Be en venn om hjelp hvis du fortsatt har problemer!
Advarsel
- Det er alltid bedre å dobbeltsjekke beregningsresultatene for å sikre at de er riktige!
- Sørg for at enhetene du bruker er de samme (cm, m, tommer, etc.) når du beregner, slik at du ikke blir feilberegnet på grunn av blandede enheter!






