- Forfatter Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Sist endret 2025-01-23 12:42.
Matematikk er vanskelig. Det er lett å glemme selv de grunnleggende konseptene når du prøver å huske de mange forskjellige prinsippene og metodene. Her er to friske måter å forenkle brøk.
Steg
Metode 1 av 4: Bruke den største fellesfaktoren

Trinn 1. Skriv ned teller- og nevnefaktorene
Faktorer er tall som du kan multiplisere for å få et annet tall. For eksempel er 3 og 4 faktorer på 12 fordi du kan multiplisere dem sammen for å få 12. For å skrive ned faktorene til et tall, trenger du bare å skrive ned alle tallene som kan multipliseres for å få det tallet, og er delbare av faktorene.
-
Skriv ned faktorene til tallet fra minste til største, uten å glemme å inkludere faktor 1. Slik skriver du for eksempel telleren og nevneren til brøkdelen 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Trinn 2. Finn den største fellesfaktoren (GCF) til telleren og nevneren
GCF er det største tallet som kan dele to eller flere tall jevnt. Etter at du har skrevet ned alle faktorene til tallet, er det bare å finne det største tallet som er det samme i begge faktorlister.
-
24: 1, 2, 3, 4, 6,
Trinn 8., 12, 24.
-
32: 1, 2, 4,
Trinn 8., 16, 32.
-
GCF på 24 og 32 er 8 fordi 8 er det største tallet som kan dele 24 og 32 jevnt.

Trinn 3. Del telleren og brøkdelen med GCF
Nå som du har GCF, er det bare å dele telleren og nevneren med dette tallet for å forenkle brøkdelen til den enkleste formen. Slik gjør du det:
- 24/8 = 3
- 32/8 = 4
- Den enkle brøkdelen er 3/4.

Trinn 4. Sjekk arbeidet ditt
Hvis du vil være sikker på at du har forenklet brøken riktig, trenger du bare å multiplisere den nye telleren og nevneren med GCF for å få den opprinnelige brøken tilbake. Slik gjør du det:
- 3 * 8 = 24
- 4 * 8 = 32
-
Du har returnert til sin opprinnelige form, som er 24/32.
Du kan også sjekke brøkdelen for å sikre at den ikke kan forenkles ytterligere. Siden 3 er et primtall, kan det bare deles med 1 og seg selv, og fire er ikke delbart med 3, så brøken kan ikke forenkles ytterligere
Metode 2 av 4: Fortsett å dele med små tall

Trinn 1. Velg et lite tall
Ved å bruke denne metoden trenger du bare å velge et lite tall, for eksempel 2, 3, 4, 5 eller 7, til å begynne med. Se på brøkene for å sikre at hver del er delelig med tallet du har valgt. For eksempel, hvis du har en brøk 24/108, ikke velg 5 fordi de ikke er delbare med 5. Men hvis du har en brøk 25/60, er 5 det riktige tallet å bruke.
For brøkdelen 24/32 er 2 et godt tall. Siden begge tallene er partall, er de delbare med 2

Trinn 2. Del telleren og nevneren til brøkdelen med tallet
Den nye brøkdelen vil bestå av en ny teller og nevner, som du får etter å ha delt toppen og bunnen av brøkdelen 24/32 med 2. Slik gjør du det:
- 24/2 = 12
- 32/2 = 16
- Den nye brøkdelen din er 12/16.
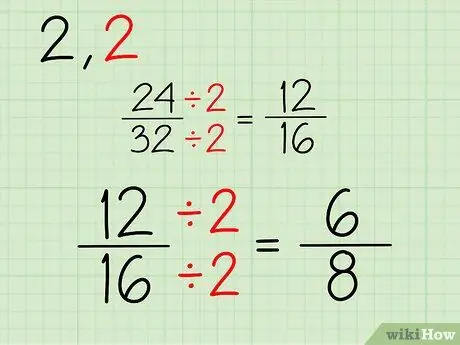
Trinn 3. Gjenta
Fortsett denne prosessen. Siden begge tallene er partall, kan du fortsette å dividere med 2. Hvis en eller begge tellerne og nevnerne er oddetall, kan du prøve å dividere med et annet tall. Her er prosessen for å forenkle fraksjonen 12/16:
- 12/2 = 6
- 16/2 = 8
- Den nye brøkdelen er 6/8.

Trinn 4. Fortsett å dele tallet til det ikke lenger er delbart
Den nye telleren og nevneren er også partall, så du kan fortsette å dele med 2. Slik gjør du det:
- 6/2 = 3
- 8/2 = 4
- Den nye brøkdelen din er 3/4.

Trinn 5. Sørg for at brøkdelen ikke kan forenkles ytterligere
I brøkdelen 3/4 er 3 et primtall, så faktorene er bare 1 og seg selv, og 4 er ikke delelig med 3, så brøken kan ikke forenkles ytterligere. Hvis telleren eller nevneren til brøken ikke lenger kan deles med tallet du valgte, kan du fortsatt dele det med et annet tall.
For eksempel, hvis du har brøkdelen 10/40, og du deler teller og nevner med 5, er resultatet 2/8. Du kan ikke fortsette å dele telleren og brøkdelen med 5, men du kan dele begge på 2 slik at sluttresultatet er 1/4

Trinn 6. Sjekk arbeidet ditt
Multipliser 3/4 med 2/2 igjen tre ganger, for å være sikker på at du får den første brøkdelen, som er 24/32. Slik gjør du det:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Legg merke til at du deler 24/32 med 2 * 2 * 2, som er det samme som å dele med 8, den største GCF på 24 og 32.
Metode 3 av 4: Skrive faktorene

Trinn 1. Skriv ned brøkdelen din
La det være et stort mellomrom på høyre side av papiret ditt - du trenger det for å skrive ned faktorene.

Trinn 2. Skriv ned faktorene til teller og nevner
Alene faktorene til de to. Den enkleste måten er at faktorene skrives oppå hverandre. Start med tallet 1 og skriv ned faktorene.
-
For eksempel, hvis brøkdelen din er 24/60, start med 24.
Skriv ned: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Deretter tallet 60.
Skriv ned: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Trinn 3. Finn og del med den største fellesfaktoren
Dette begrepet kan skrives som GCF i den trykte boken din. Hva er det største tallet som kan dele teller og nevner? Uansett tallet, del begge tallene med det tallet.
For vårt eksempel er det største tallet som er en faktor for begge tallene 12. Dermed deler vi 24 med 12 og 60 med 12, og gir oss 2/5 - vår enkle brøk
Metode 4 av 4: Bruke et Prime Factor Tree

Trinn 1. Finn hovedfaktorene til teller og nevner
Et primtall er et tall som ikke kan deles med noe annet tall (annet enn seg selv og 1, selvfølgelig). 2, 3, 5, 7 og 11 er eksempler på primtall.
- Start med telleren. Fra 24, delt i 2 og 12. Siden 2 allerede er et primtall, trenger du ikke dele det lenger! Del deretter 12 i 2 tall: 2 og 6. 2 er primtall - flott! Del nå 6 i 2 tall: 2 og 3. Du har nå 2, 2, 2 og 3 som primtall.
- Nå jobber du med nevneren. Fra 60, del treet ditt i 2 og 30. 30 del deretter inn i 2 og 15. Del deretter 15 i 3 og 5, som begge er primtall. Nå har du 2, 2, 3 og 5 som primtall.
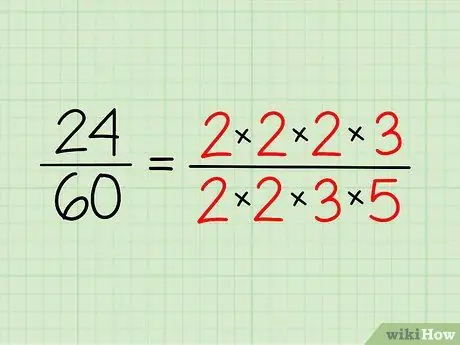
Trinn 2. Skriv ned primfaktoriseringen av hvert tall
Skriv ned primtallene du har for hvert tall, og skriv dem i form for multiplikasjon. Du trenger ikke å multiplisere det - det er bare en måte å gjøre det lettere å se.
- Så for 24 har du 2 x 2 x 2 x 3 = 24.
- For 60 har du 2 x 2 x 3 x 5 = 60

Trinn 3. Eliminer de samme faktorene
Ethvert nummer som er en del av begge tallene kan kastes. I dette eksemplet er like faktorer et par 2er og en 3. Farvel!
- Resten er 2 og 5 - eller 2/5! Det samme svaret fikk vi veien ovenfor.
- Hvis brøkets teller og nevner er partall, ikke bare dele med to. Fortsett å gjøre divisjonen til tallet du får ikke kan deles igjen.






