- Forfatter Jason Gerald [email protected].
- Public 2024-01-15 08:21.
- Sist endret 2025-01-23 12:42.
Å dele en brøkdel med en brøkdel kan virke forvirrende i begynnelsen, men det er faktisk veldig enkelt. Alt du trenger å gjøre er å snu, multiplisere og forenkle! Denne artikkelen vil lede deg gjennom prosessen og vise deg hvor enkelt det er å dele en brøkdel med en brøkdel.
Steg
Del 1 av 2: Forstå hvordan man deler brøk med brøk
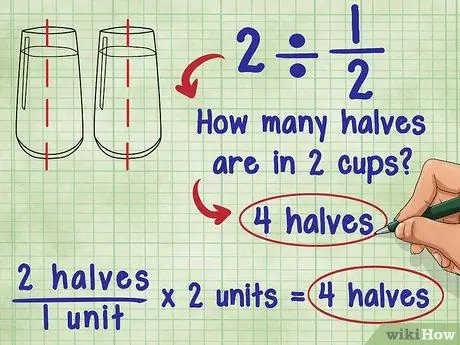
Trinn 1. Tenk på hva det å dele med en brøk betyr
Om 2 ÷ 1/2 spurte Ada: "Hvor mange halvdeler er i to?" Svaret er 4 fordi hver enhet (1) består av to "halvdeler", og det er to enheter totalt: 2 "halv"/1 enhet * 2 enheter = 4 "halvdel".
- Prøv å forestille deg den samme ligningen ved å bruke et glass vann: Hvor mange og et halvt glass vann er i 2 glass vann? Du kan helle 2 og en halv kopp vann i hvert glass vann. Det betyr at du i utgangspunktet legger opp de "halve" glassene med vann, og du har to glass: 2 "halv"/1 kopp * 2 kopper = 4 "halv".
- Dette betyr at hvis brøkdelen du deler er mellom 0 og 1, er svaret alltid større enn det opprinnelige tallet! Dette er sant når du deler et helt tall eller brøk med en brøk.

Trinn 2. Forstå at deling er det motsatte av å multiplisere
Dermed kan dividere med en brøk løses ved å multiplisere med gjensidig av fraksjonen. Gjensidigheten til en brøk (også kalt "multiplikasjonsinversen") er brøken som er invertert, slik at teller og nevner bytter plass. Om et øyeblikk vil vi dele brøk med brøk, ved å finne den gjensidige av den andre fraksjonen og multiplisere begge brøkene. La oss imidlertid først se på noen av motsetningene:
- Det gjensidige av 3/4 er 4/3.
- Det motsatte av 7/5 er 5/7.
- Det gjensidige av 1/2 er 2/1 eller 2.
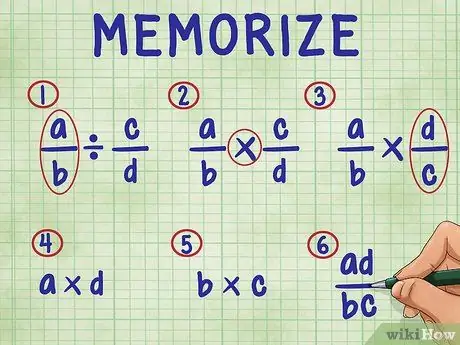
Trinn 3. Husk følgende trinn for å dele en brøk med en brøk
I rekkefølge inkluderer trinnene:
- Bare la den første brøkdelen være i ligningen.
- Endre divisjonstegnet til multiplikasjonstegnet.
- Vend den andre fraksjonen (finn den gjensidige).
- Multipliser telleren (toppnummer) for begge brøkene. Multiplikasjonsresultatet er telleren (øverst) på svaret ditt.
- Multipliser nevneren (bunnnummer) for begge brøkene. Produktet av produktet er nevneren for svaret ditt.
- Forenkle brøkene dine ved å forenkle dem til deres enkleste vilkår.
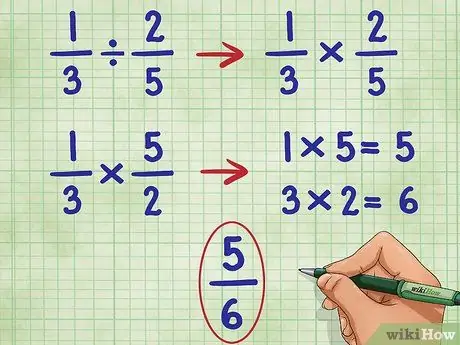
Trinn 4. Utfør disse trinnene for 1/3 2/5 eksemplet
Vi starter med å utelate den første fraksjonen og konvertere divisjonstegnet til multiplikasjonstegnet:
- 1/3 ÷ 2/5 = Blir:
- 1/3 * _ =
- Nå reverserer vi den andre fraksjonen (2/5) for å finne den gjensidige, som er 5/2:
- 1/3 * 5/2 =
- Nå multipliserer du telleren (toppnummer) av begge brøkene, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Nå multipliserer nevneren (bunnnummer) for begge brøkene, 3*2 = 6.
- Nå har vi: 1/3 * 5/2 = 5/6
- Denne brøkdelen kan ikke forenkles ytterligere, så vi har vårt svar.

Trinn 5. Prøv å huske følgende rim for å hjelpe deg med å huske:
"Det er enkelt å dele brøk, reverser den andre fraksjonen, og multipliser deretter. Ikke glem å forenkle før det er på tide å spise."
En annen nyttig påminnelseshjelp forteller deg hva du skal gjøre med hver del av ligningen: "La meg (første brøk), Endre meg (divisjonstegn), Inverter meg (andre brøk)."
Del 2 av 2: Deling av brøk etter brøk i problemer
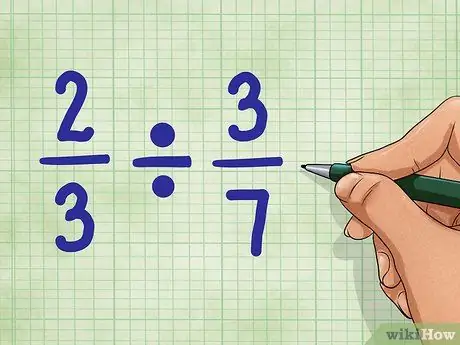
Trinn 1. Start med eksempler på spørsmål
La oss bruke 2/3 ÷ 3/7. Dette spørsmålet ber om antall deler lik 3/7, som finnes i verdien 2/3. Ikke bekymre deg. Det er ikke så vanskelig som det høres ut!
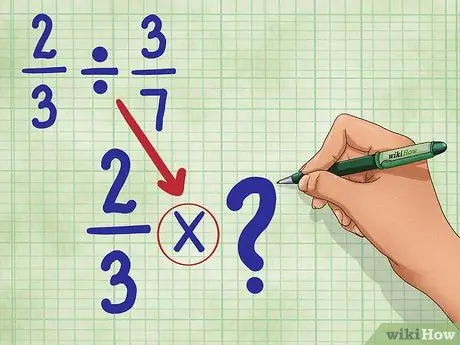
Trinn 2. Konverter divisjonstegnet til multiplikasjonstegnet
Din nye ligning vil være: 2/3 * _ (Vi fyller dette emnet om et øyeblikk.)
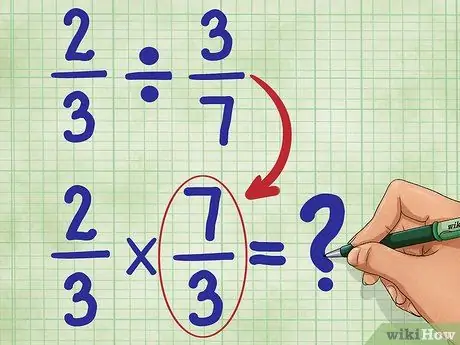
Trinn 3. Finn nå det gjensidige av den andre fraksjonen
Dette betyr å snu 3/7 slik at telleren (3) nå er nederst, og nevneren (7) nå er øverst. Det gjensidige av 3/7 er 7/3. Skriv nå din nye ligning:
2/3 * 7/3 = _

Trinn 4. Multipliser brøkene dine
Multipliser først tellerne for begge brøkene: 2 * 7 = 14. 14 er telleren (toppnummeret) på svaret ditt. Multipliser deretter nevnerne til begge brøkene: 3 * 3 = 9. 9 er nevneren (nederste tall) for svaret ditt. Nå vet du det 2/3 * 7/3 = 14/9.
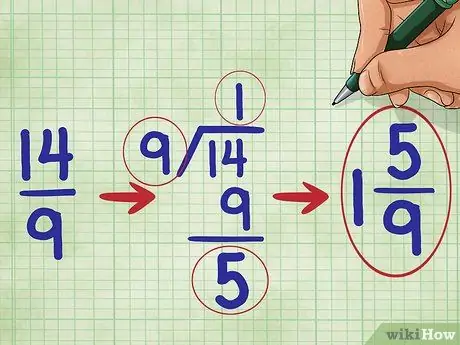
Trinn 5. Forenkle brøkdelen din
I dette problemet, fordi telleren av brøken er større enn nevneren, vet vi at vår brøk er større enn 1. Vi må konvertere den til et blandet tall. (Et blandet tall er et helt tall og en brøk kombinert, for eksempel 1 2/3.))
-
Del først telleren
Trinn 14. med 9.
Tallet 14 delt på 9 er lik ett med resten av 5, så du bør skrive ned din forenklede brøk som: 1 5/9 ("En fem-niende").
- Stopp, du har funnet svaret! Du kan angi at du ikke kan forenkle brøken lenger fordi nevneren ikke er delelig med telleren (9 er ikke delelig med 5) og telleren er et primtall, eller et heltall som bare er delbart med ett og selve tallet.
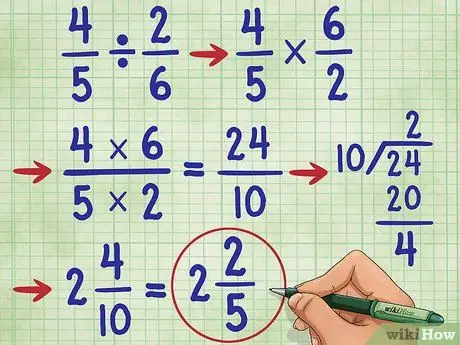
Trinn 6. Prøv et annet eksempel
La oss prøve spørsmålet 4/5 ÷ 2/6 =. Endre først divisjonstegnet til multiplikasjonstegnet (4/5 * _ =), og finn deretter det gjensidige av 2/6, som er 6/2. Nå har du ligningen: 4/5 * 6/2 =_. Nå, multipliser telleren, 4 * 6 = 24, og nevneren 5* 2 = 10. Nå har du det 4/5 * 6/2 = 24/10.
Forenkle brøkdelen nå. Siden telleren er større enn nevneren, må vi konvertere denne brøkdelen til et blandet tall.
- Del først telleren med nevneren, (24/10 = 2 gjenværende 4).
- Skriv svaret som 2 4/10. Vi kan fortsatt forenkle denne brøkdelen igjen!
- Vær oppmerksom på at 4 og 10 er partall. Så det første trinnet for å forenkle det er å dele hvert tall med 2. Vi får 2/5.
- Siden nevneren (5) ikke er delelig med telleren (2) og 5 er et primtall, vet vi at denne brøkdelen ikke kan forenkles ytterligere. Så, vårt svar er: 2 2/5.

Trinn 7. Få ytterligere hjelp til å forenkle brøk
Du har sannsynligvis brukt mye tid på å lære å forenkle brøker før du prøver å dele dem med hverandre. Men hvis du trenger en oppfriskning eller annen hjelp, er det noen flotte artikler på nettet som kan være til stor hjelp for deg.
Relaterte wikiHow -artikler
- Konvertering av vanlige brøker til desimaler
- Beregning av arealet til en sirkel
- Deling av polynomer ved hjelp av syntetisk divisjon
- Deling av blandede fraksjoner






