Å dele brøk med hele tall er ikke så vanskelig som det virker. For å dele en brøk med et heltall, er alt du trenger å gjøre å konvertere hele tallet til en brøk, finne brøkens gjensidige og multiplisere resultatet med den første brøken. Hvis du vil vite hvordan du gjør det, følger du bare disse trinnene:
Steg
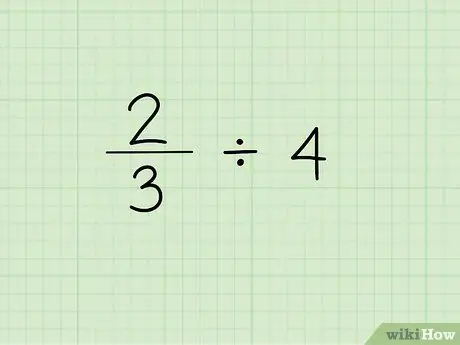
Trinn 1. Skriv ned problemet
Det første trinnet for å dele en brøk med et heltall er å skrive brøken etterfulgt av divisjonstegnet og heltallet du trenger for å dele brøkdelen. La oss si at vi jobber med følgende problem: 2/3 4.
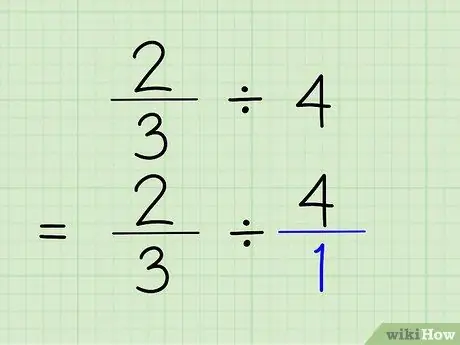
Trinn 2. Konverter heltall til brøk
For å konvertere et helt tall til en brøk, er alt du trenger å gjøre å plassere heltallet over tallet 1. Heltallet blir teller og 1 blir nevneren til brøken. Å si 4/1 er egentlig det samme som å si 4, fordi du bare viser at tallet inneholder "1" 4 ganger. Problemet vil være 2/3 4/1.
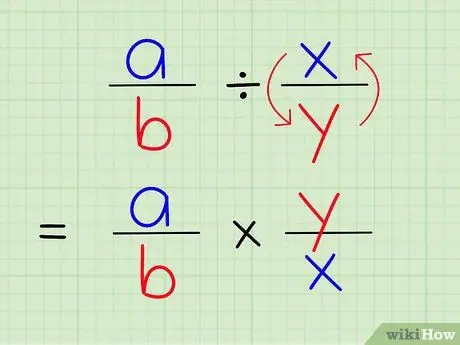
Trinn 3. Å dele en brøk med en annen er det samme som å multiplisere den med den gjensidige av en annen brøk
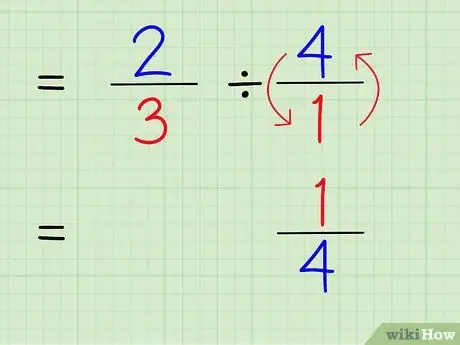
Trinn 4. Skriv gjensidigheten til heltallet
For å finne det gjensidige av et tall, bytt teller og nevner av tallet. Derfor, for å finne det gjensidige av 4/1, bytter du bare teller og nevner slik at tallet blir 1/4.
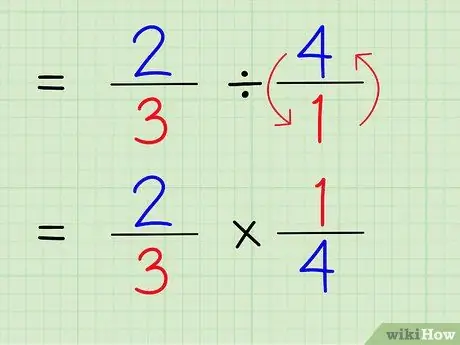
Trinn 5. Endre divisjonstegnet til multiplikasjonstegnet
Problemet vil være 2/3 x 1/4.
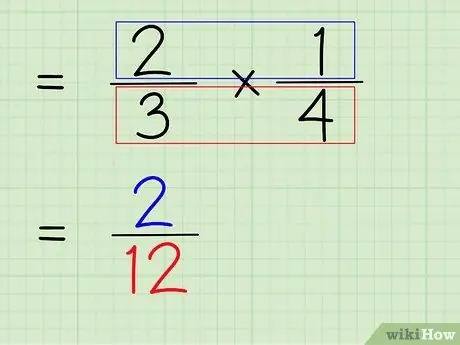
Trinn 6. Multipliser telleren og nevneren til brøkdelen
Så det neste trinnet er å multiplisere telleren og nevneren til brøkdelen for å få en ny teller og nevner som det endelige svaret.
- For å multiplisere tellerne, bare multipliser 2 x 1 for å få 2.
- For å multiplisere nevnerne, multipliserer du bare 3 x 4 for å få 12.
- 2/3 x 1/4 = 2/12
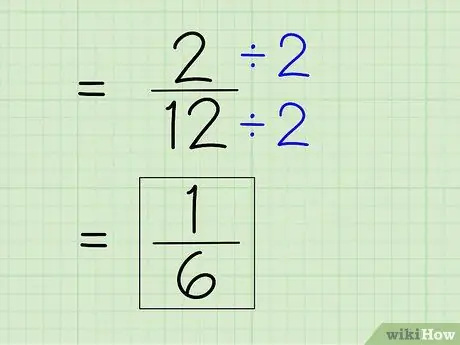
Trinn 7. Forenkle brøkdelen
For å forenkle en brøk, må du finne den minste nevneren, noe som betyr at du må dele teller og nevner med et hvilket som helst tall som deler begge tallene. Siden 2 er telleren, må du se om 2 kan dele 12 helt - det kan fordi 12 er et partall. Del deretter teller og nevner med 2 for å få en ny teller og nevner for å få et enkelt svar.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- Fraksjonen 2/12 kan forenkles til 1/6. Dette er ditt endelige svar.
Tips
- Dette er for å hjelpe minnet, en enkel måte å huske hvordan du gjør alle disse beregningene. Husk dette: "Det er lett å dele brøk, reversere det andre tallet og multiplisere!"
- En annen variant av metoden ovenfor er JGB/JBG. Ikke endre det første tallet. Bytt til multiplikasjon. Snu det siste tallet. Eller B først deretter G.
- Hvis du avbryter beregningen før du multipliserer den, trenger du kanskje ikke finne den enkleste formen for brøken fordi resultatet allerede er i den enkleste brøkformen som du kan se. I vårt eksempel, før vi multipliserer 2/3 × 1/4, kan vi se at den første telleren (2) og den andre nevneren (4) har samme multiplikator på 2, som vi kan avbryte før vi fortsetter beregningen. Dette konverterer problemet til 1/3 × 1/2, noe som gir et umiddelbart 1/6 resultat og sparer oss tid for å forenkle brøken på et senere tidspunkt.
- Hvis en av brøkene dine er negativ, er denne metoden fremdeles brukbar; sørg for å holde oversikt over skiltene mens du utfører disse trinnene.
