- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:21.
- Sist endret 2025-01-23 12:42.
Å dele med desimaltall virker vanskelig i begynnelsen fordi ingen har lært deg "0, 7 ganger tabellen". Hemmeligheten bak dette er å konvertere divisjonsproblemet til et format som bare bruker hele tall. Etter at du har skrevet om problemet på denne måten, blir det et vanlig langdivisjonsproblem.
Steg
Del 1 av 2: Skriveproblemer som vanlige delingsproblemer
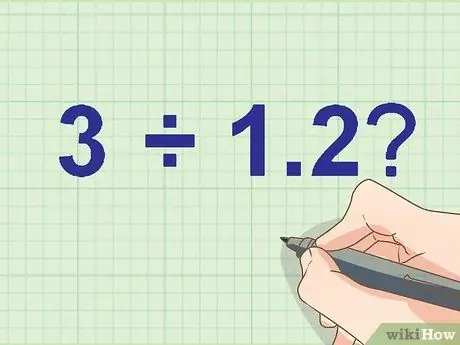
Trinn 1. Skriv ned delingsproblemet ditt
Bruk en blyant hvis du vil forbedre arbeidet ditt.
-
Eksempel:
Hvor mange 3 ÷ 1, 2?

Trinn 2. Skriv hele tallet som en desimal
Skriv et desimalpunkt etter hele tallet, og skriv deretter et null etter desimaltegnet. Gjør dette til begge tallene har samme stedsverdi til høyre for desimaltegnet. Dette endrer ikke heltallsverdien.
-
Eksempel:
I oppgaven 3 1, 2 er hele tallet vårt 3. Siden 1, 2 har en stedsverdi til høyre for desimaltegnet, skriv 3 som 3, 0 slik at dette tallet også har én stedsverdi etter desimalen. Nå blir saken vår 3, 0 ÷ 1, 2.
- Advarsel: ikke legg til nuller til venstre for desimaltegnet! Tallet 3 er lik 3, 0 eller 3, 00, men ikke lik 30 eller 300.

Trinn 3. Flytt desimaltegnet til høyre til du får et helt tall
I divisjonsproblemer kan du flytte desimalpunktene, men bare hvis du flytter desimalpunktene på alle tallene med samme antall trinn. Dette lar deg konvertere problemet til et helt tall.
-
Eksempel:
For å konvertere 3, 0 1, 2 til et helt tall, flytt desimaltegnet ett trinn til høyre. Dermed blir 3, 0 30 og 1, 2 blir 12. Nå blir vårt problem 30 ÷ 12.

Trinn 4. Skriv problemet ved å bruke lang divisjon
Plasser det delbare tallet (vanligvis det større tallet) under symbolet for lang divisjon. Skriv delerenummeret utenfor dette symbolet. Nå har du et vanlig langdivisjonsproblem som bruker hele tall. Hvis du vil ha en påminnelse om hvordan du gjør lang divisjon, kan du lese neste avsnitt.
Del 2 av 2: Løse problemer med lange divisjoner

Trinn 1. Finn det første sifferet i svaret
Begynn å løse dette problemet på samme måte som du vanligvis ville, ved å sammenligne divisoren og det første sifferet i det delte tallet. Beregn resultatet av å dele dette første sifferet med nummeret til divisoren, og skriv deretter resultatet over det sifferet.
Eksempel: Vi prøver å dele 30 med 12. Sammenlign 12 med det første sifferet i tallet delt, som er 3. Siden 12 er større enn 3, er 3 dividert med 12 lik 0. Skriv ned 0 over 3 i svarlinjen.
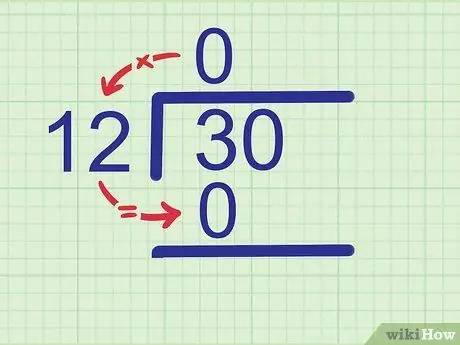
Trinn 2. Multipliser kvoten med divisoren
Skriv produktet av produktet under tallet som er delt. Skriv resultatet like under det første sifferet i tallet du delte fordi dette er sifferet du nettopp så.
-
Eksempel:
Siden 0 x 12 = 0, skriv 0 under 3.
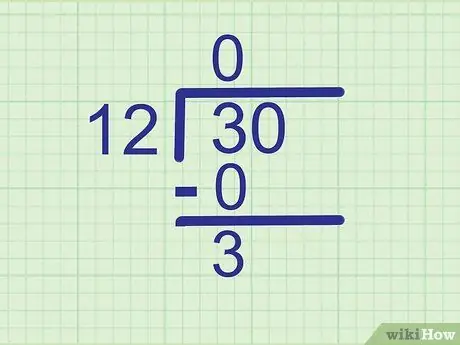
Trinn 3. Trekk fra for å finne resten
Trekk produktet du nettopp har beregnet fra tallet rett over det. Skriv svaret på en ny linje, under den.
-
Eksempel:
3 - 0 = 3, så skriv
Trinn 3. like under 0.
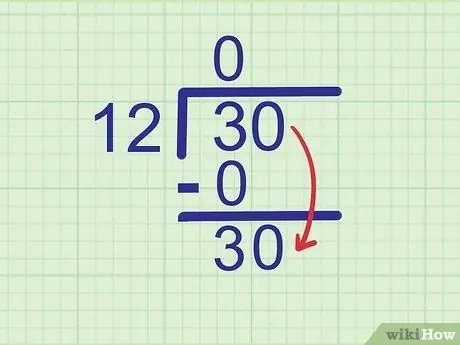
Trinn 4. Senk det neste sifferet
Slipp det neste sifferet i det delte tallet ved siden av tallet du nettopp skrev ned.
-
Eksempel:
Tallet som er delt er 30. Vi har sett tallet 3, så neste siffer som må senkes er 0. Reduser tallet 0 til siden av 3 slik at det blir
Trinn 30..
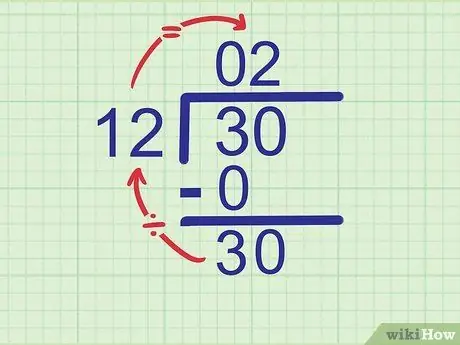
Trinn 5. Prøv å dele det nye tallet med divisoren
Gjenta det første trinnet i denne delen for å finne det andre sifferet i svaret ditt. Denne gangen sammenligner du divisoren med tallet du nettopp skrev ned på nederste rad.
-
Eksempel:
Hva er kvoten 30 til 12? Det nærmeste svaret vi kan få er 2 fordi 12 x 2 = 24. Skriv
Steg 2. på andreplass på svarlinjen.
- Hvis du ikke er sikker på svaret, kan du prøve flere multiplikasjoner til du finner det største svaret som passer. For eksempel, hvis estimatet er 3, beregner du 12 x 3 og du får 36. Dette tallet er for stort fordi vi prøver å beregne 30. Prøv å senke ett tall, 12 x 2 = 24. Dette tallet passer. Så 2 er det riktige svaret.

Trinn 6. Gjenta trinnene ovenfor for å finne det neste nummeret
Dette er den samme lange delingsprosessen som brukt ovenfor, og for alle lange delingsproblemer:
- Multipliser det nye sifferet i svaret ditt med divisoren: 2 x 12 = 24.
- Skriv produktet på en ny linje, under tallet som ble delt: Skriv 24 like under 30.
- Trekk den nederste raden fra raden over den: 30 - 24 = 6. Så skriv 6 i en ny rad under den.

Trinn 7. Fortsett denne prosessen til du har fullført den siste linjen med svar
Hvis det fortsatt er sifre igjen i det delte tallet, senker du sifrene ned og fortsetter å løse problemet på samme måte. Hvis du har fullført den siste linjen med svar, fortsetter du til neste trinn.
-
Eksempel:
Vi skrev nettopp
Steg 2. i siste svarlinje. Fortsett til neste trinn.

Trinn 8. Legg til desimaler for å "utvide" det delte tallet om nødvendig
Hvis tallet er jevnt delbart, er det endelige subtraksjonsresultatet “0”. Det betyr at du er ferdig med å dele og du får svar i form av et helt tall. Men hvis du har fullført den siste linjen med svar og det fortsatt er tall som kan deles, må du "utvide" det delbare tallet ved å legge til et desimaltegn etterfulgt av tallet 0. Husk at dette ikke gjør det ikke endre verdien på tallet.
-
Eksempel:
Vi har kommet til den siste linjen med svar, men svaret på vår siste subtraksjon er "6". Skriv “6, 0” under symbolet for lang divisjon ved å legge til “, 0” til det siste sifferet. Skriv også desimaltegnet på samme sted på svarlinjen, men ikke skriv noe etter det.

Trinn 9. Gjenta de samme trinnene for å finne det neste sifferet
Den eneste forskjellen her er at du må legge til desimaltegnet til samme sted på svarlinjen. Når du har gjort det, kan du søke etter de gjenværende svarstallene på nøyaktig samme måte.
-
Eksempel:
Slipp den nye 0 -en ned til den siste linjen slik at den blir “60”. Siden 60 delt på 12 er nøyaktig 5, skriv
Trinn 5. som det siste sifferet i svarlinjen vår. Ikke glem at vi setter en desimal i svarlinjen. Så, 2, 5 er det endelige svaret på spørsmålet vårt.
Tips
- Du kan skrive dette som en rest (så svaret på 3 1, 2 er “2 gjenværende 6”). Men fordi du jobber med desimaler, kan læreren din forvente at du jobber med desimaldelen av svaret.
- Hvis du følger metoden for lang divisjon riktig, har du alltid et desimaltegn i riktig posisjon, eller ingen desimal i det hele tatt hvis tallet er delbart med delbart. Ikke prøv å gjette desimalene. Desimalen er ofte forskjellig fra desimalen i startnummeret ditt.
- Hvis problemet med lang divisjon ikke varer lenge, kan du stoppe og runde til nærmeste nummer. For eksempel, for å løse 17 4, 2, teller du bare til 4,047 … og avrunder svaret ditt til "omtrent 4,05".
-
Husk delingsbetingelsene:
- Tallet som skal deles er tallet som skal deles.
- Deleren er tallet som brukes til å dele.
- Kvotienten er svaret på matematikkinndelingsproblemet.
- Hele: Delt med Divisor = kvotient.
Advarsel
Husk at 30 12 vil gi det samme svaret som 3 1, 2. Ikke prøv å "rette" svaret ditt etter å ha flyttet desimalen bakover
Relaterte wikiHow -artikler
- Konvertering av vanlige brøker til desimaler
- Gjør langbestemt divisjon
- Del brøk med brøk
- Deling av blandede fraksjoner






