- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:30.
- Sist endret 2025-01-23 12:42.
Å telle brøk er en av de mest nyttige matematiske ferdighetene å utvikle. Lær hvordan du identifiserer deler og typer fraksjoner før du utfører brøkberegninger. Etter det kan du legge til eller trekke dem fra. For mer komplekse beregninger, lær hvordan du multipliserer og deler brøker. Vanligvis må du også forenkle eller redusere brøk.
Steg
Metode 1 av 4: Gjenkjenning av brøker

Trinn 1. Finn brøkdelen
Brøker skrives som ett tall over skillelinjen, og et annet tall under linjen.
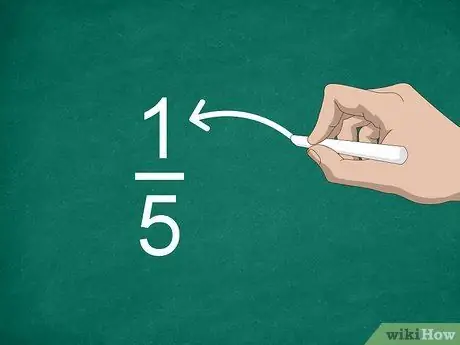
Trinn 2. Identifiser telleren
Tallet over linjen kalles teller og viser hvor mange deler det er i brøkdelen.
For eksempel, i brøkdelen 1/5, er “1” telleren
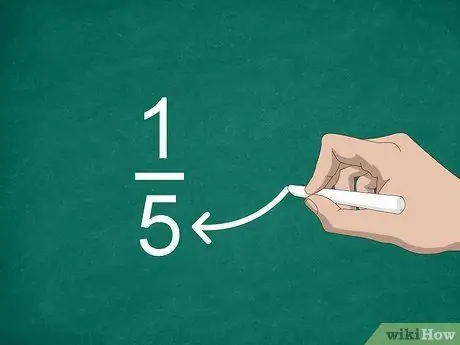
Trinn 3. Finn nevneren
Tallet plassert under linjen kalles nevner. Denne verdien angir antall deler som "konstruerer" et heltall.
For eksempel, i brøkdelen 1/5, er "5" nevneren, så det er fem deler til fraksjonen

Trinn 4. Bestem om brøkene er rimelige fraksjoner eller feil brøk
Hvis telleren er mindre enn nevneren, er brøkdelen en naturlig brøk. I feil brøk er telleren større enn nevneren.
- For eksempel er 3/4 en rimelig brøk og 5/3 er en feil brøk.
- Hvis du har et heltall som inneholder en brøk, er tallet kjent som et blandet tall. For eksempel er 1 1/2 et blandet tall.
Metode 2 av 4: Legg til eller trekk fra fraksjoner

Trinn 1. Identifiser brøker med samme nevner
Hvis du trenger å legge til eller trekke fra brøk, må hver brøk ha samme nevner før du utfører beregningen. Observer nevneren til hver brøk for å sikre at de alle er like (like).
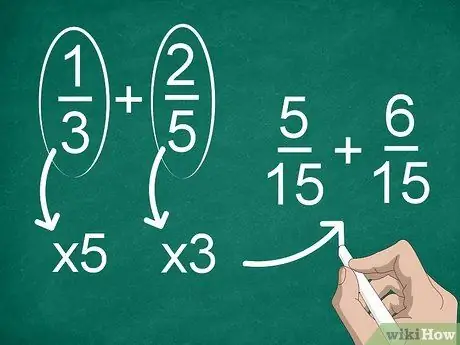
Trinn 2. Finn en fellesnevner hvis hver brøk har en annen nevner
Hvis nevnerne ikke er de samme, må du endre brøkene for å ha den samme nevneren. For å finne en fellesnevner, multipliser hver brøk med nevneren til den andre.
For eksempel, for å finne en fellesnevner i 1/3 + 2/5, multipliserer "1" og "3" med "5", deretter multipliserer "2" og "5" med "3". Nå har du tillegg av 5/15 + 6/15. Etter det kan du beregne brøkene
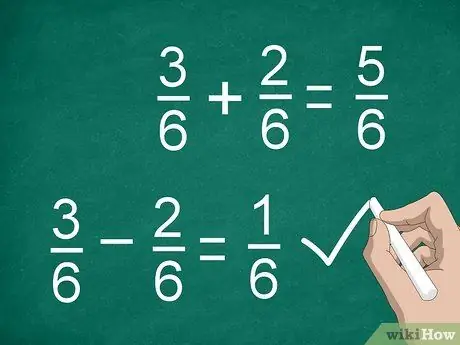
Trinn 3. Legg til eller trekk tellerne for å beregne brøk
Når du har funnet en fellesnevner og multiplisert tellerne (om nødvendig), er du klar til å legge til eller trekke fra. Legg til eller trekk fra tellerne og plasser resultatet over skillelinjen. Skriv fellesnevneren under streken.
- For eksempel 3/6 - 2/6 = 1/6.
- Ikke legg til eller trekk nevnerne.
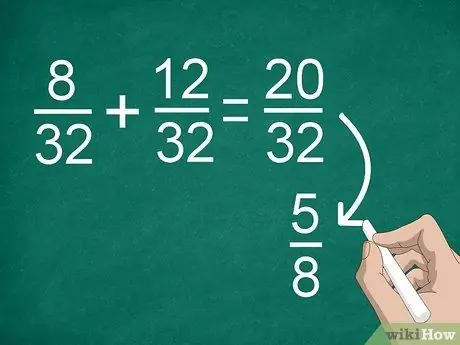
Trinn 4. Forenkle resultatene om nødvendig
Hvis du tidligere måtte finne en fellesnevner, kan du få en stor brøkdel som du kan forenkle. For eksempel, hvis du legger til 8/32 +12/32, får du “20/32” som resultat. Denne brøkdelen kan forenkles til “5/8”.
Metode 3 av 4: Multiplisere og forenkle brøk
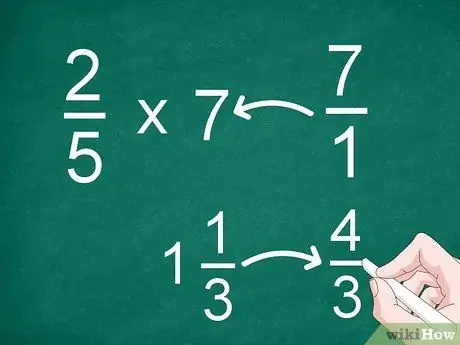
Trinn 1. Konverter blandede fraksjoner eller heltall til feil brøk
For å gjøre multiplikasjon enklere må du konvertere hvert tall til en rimelig eller feil brøk. Hvis du har hele tall eller blandede tall som må multipliseres, må du først konvertere dem til en vanlig brøk (naturlig eller feil).
- For eksempel, for å multiplisere 2/5 med 7, konverter "7" til en brøk. Etter det kan du multiplisere 2/5 med 7/1.
- Hvis du har et blandet tall som 1 1/3, konverter det til en feil brøk (“4/3”) før du multipliserer.
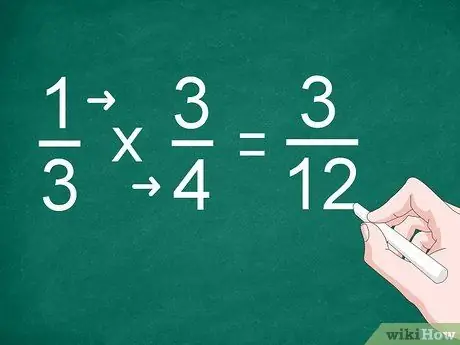
Trinn 2. Multipliser hver teller og nevner
I stedet for å gjøre tillegg, multipliserer du telleren og skriver resultatet over skillelinjen. Du må også multiplisere nevnerne og skrive resultatet under linjen.
For eksempel, for å multiplisere 1/3 med 3/4, multipliserer "1" med "3" for å få telleren. Multipliser "3" med "4" for å få nevneren. Svaret på multiplikasjonen er "3/12"

Trinn 3. Forenkle resultatene
Vanligvis må du redusere resultatet til en enklere form, spesielt hvis du i utgangspunktet har unaturlige brøk. Finn den største fellesfaktoren og bruk denne faktoren for å forenkle telleren og nevneren.
For brøkdelen 3/12 er for eksempel den største fellesfaktoren mellom “3” og “12” “3”. Del hvert element av brøkdelen med "3" til du får brøkdelen "1/4"
Metode 4 av 4: Del fraksjoner
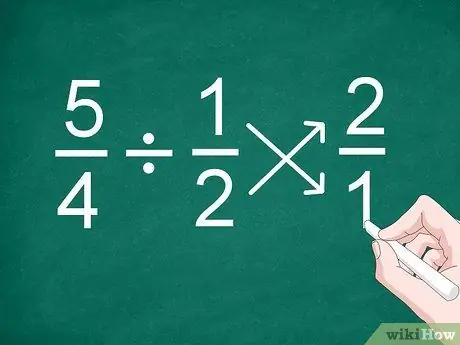
Trinn 1. Snu posisjonen til den andre fraksjonen
Den enkleste måten å dele brøk på, til og med brøk med forskjellige nevnere, er å reversere posisjonen til den andre fraksjonen før du beregner resultatet.
For eksempel, for problemet 5/4 1/2, snu posisjonen til brøkdelen "1/2" for å bli "2/1"
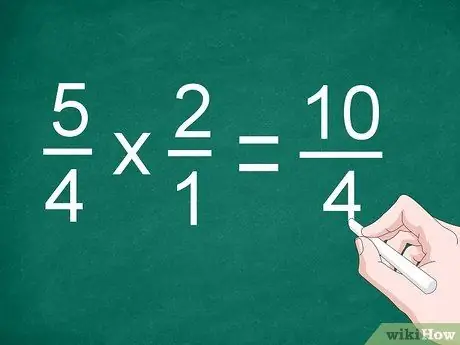
Trinn 2. Multipliser teller og nevner
Multipliser brøker direkte for å multiplisere tellerne. Skriv resultatet over skillelinjen, og multipliser nevneren. Noter produktet av nevnerne under linjen.
For det forrige eksemplet, multipliser 5/4 med 2/1 for å få “10/4”
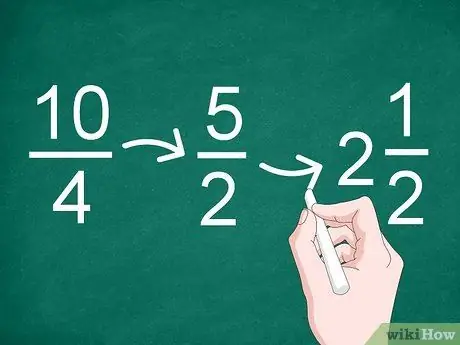
Trinn 3. Forenkle resultatene om nødvendig
Hvis resultatet av divisjonen er en feil brøkdel eller kan reduseres, forenkle brøkdelen. Bruk den største fellesfaktoren for å redusere brøkdelen.
- For eksempel er den største fellesfaktoren i brøkdelen 10/4 “2”, så resultatet av forenklingen blir “5/2” (10 delt på 2 og 4 delt på 2).
- Siden resultatet av forenklingen er en feil brøk, kan du konvertere den til et heltall og en brøk (et blandet tall). Derfor kan 5/2 endres til “2”.
Tips
- Hvis du jobber med komplekse brøker, må du ta noen ekstra trinn for å forenkle brøken. Imidlertid er selve forenklingen en obligatorisk del av beregningsprosessen.
- Skriv alltid brøkene pent for å redusere risikoen for feilberegninger.






