- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:30.
- Sist endret 2025-01-23 12:42.
Hvis du allerede forstår, er det ikke vanskelig å konvertere vanlige brøk til desimaler. For å konvertere vanlige brøk til desimaler, kan du bruke lang divisjon, multiplikasjon eller til og med en kalkulator hvis du ikke vil beregne for hånd. Når du har mestret metoden, kan du enkelt konvertere brøk til desimaler.
Steg
Metode 1 av 4: Med lang divisjon
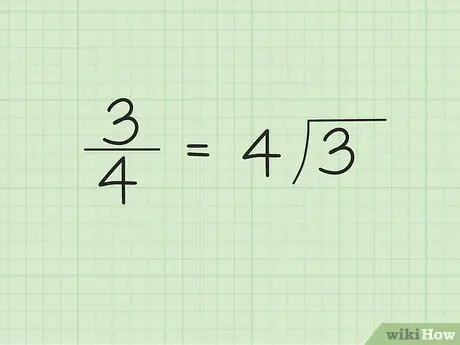
Trinn 1. Skriv nevneren utenfor/venstre side av divisorsymbolet og telleren inne/høyre side av divisorsymbolet
La oss for eksempel si at vi vil konvertere 3/4 til en desimal. Skriv “4” utenfor/venstre side av divisorsymbolet og “3” inne/høyre side av divisorsymbolet. “4” er tallet som deler seg og “3” er tallet som er delt.

Trinn 2. Skriv “0”, deretter et desimaltegn (et komma), over divisorsymbolet
Siden det er en brøkdel som teller, må resultatet være mindre enn ett, så dette trinnet er veldig viktig. Etter det skriver du desimaltegnet, deretter “0”, etter tallet “3” i/høyre side av divisorsymbolet. Selv om "3" er lik "3, 0", tillater nullen at "3, 0" deles med "4".

Trinn 3. Beregn svaret ved å bruke lang divisjon
Med lang divisjon kan desimaltegnet foreløpig ignoreres, så du trenger bare å beregne 30 dividert med 4. Slik gjør du:
- Del først 3, 0, som teller som 30, med 4. Den nærmeste 4 til 30 er 4 x 7 = 28, forlater 2. Så skriv "7" etter "0", over divisoren og "28" under " 3, 0”i/høyre side av delersymbolet. Under 28 skriver du "2", resten av 30 minus 28.
- Skriv deretter “0” etter “3, 0” slik at det blir “3, 00”, som kan betraktes som “300”, inne/høyre side av divisorsymbolet. Dermed kan 0 senkes til høyre for "2" slik at "20" er delelig med "4".
- "20" delt på "4" er lik "5". Så skriv "5" etter "0,7" over divisorsymbolet slik at det blir "0,75".

Trinn 4. Skriv det endelige svaret
Så "3" dividert med "4" er lik "0,75". Skriv ned svaret. Ferdig.
Metode 2 av 4: Fraksjoner som genererer gjentagende desimaler
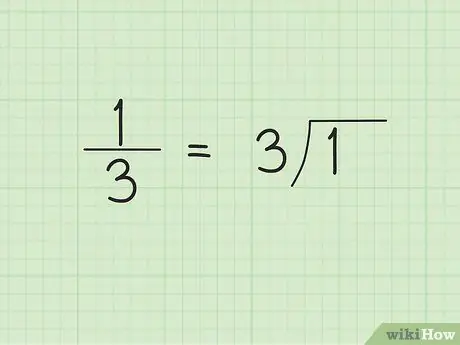
Trinn 1. Lag lang divisjon
Når du starter langsifret divisjon, er det ikke sikkert du kan forutsi at resultatet blir et gjentakende desimaltall. La oss for eksempel si at vi vil konvertere den vanlige brøkdelen 1/3 til desimalform. Skriv 3, eller nevneren, på utsiden/venstre side av divisorsymbolet og 1 innside/høyre side av divisorsymbolet.

Trinn 2. Skriv et 0, deretter et desimaltegn, over divisorsymbolet
Siden resultatet må være mindre enn 1, forbereder dette trinnet at svaret skrives i desimalform. Desimaltegnet må også skrives til høyre for tallet “1” som er plassert i/høyre side av divisorsymbolet.
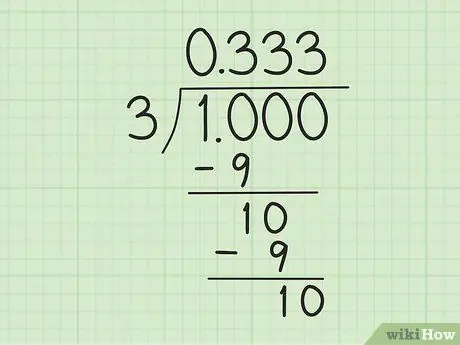
Trinn 3. Begynn å beregne divisjon med lang divisjon
Start med å gjøre “1” til “1, 0”, som teller som “10”, slik at den er delelig med “3”. Utfør deretter følgende trinn:
- Del 10 med 3. Bruk 3 x 3 = 9 for å lage resten av 1. Så skriv 3 til høyre for "0", over divisorsymbolet og trekk 10 med 9 for å få resten av 1.
- Skriv en "0" til høyre for tallet "1" (resten av 10 minus 9 i forrige trinn) nedenfor for å få en annen "10". Når du igjen deler "10" med "3", gjentas den samme prosessen: skriv "3" til høyre for den første "3" over divisorsymbolet og trekk den nye "10" med "9".
- Fortsett til et mønster dannes. Vet du at noe er rart? Denne inndelingen kan fortsette for alltid. 10 er alltid delelig med 3: det vil alltid være en "1" nederst og en ny "3" etter desimalen over divisorsymbolet.
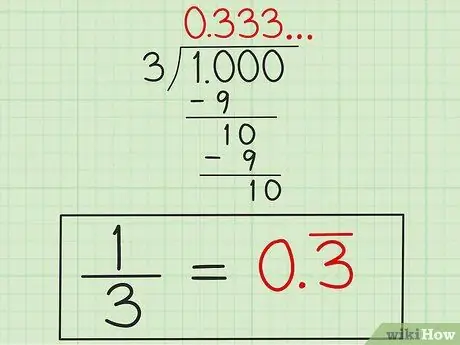
Trinn 4. Skriv svaret
Etter å ha visst at "3" vil gjenta seg selv, skriver du svaret som "0, 3" med en linje over tallet "3" (eller "0, 33" med en linje over begge tallene "3") som en indikasjon på at nummeret "3" blir det gjentatt. Dette svaret er i desimalform 1/3 fordi 1 delt på 3 ikke vil ende av seg selv.
Det er mange brøk som produserer gjentagende desimaler, for eksempel 2/9 (“0, 2” med “2” repeterende), 5/6 (“0, 83” med “3” repeterende) eller 7/9 (“0, 7”med“7”gjentas stadig). Dette mønsteret oppstår alltid når nevneren er et multiplum av 3 og telleren ikke kan deles med nevneren
Metode 3 av 4: Ved multiplikasjon

Trinn 1. Finn tallet som kan multipliseres med nevneren til brøkdelen for å produsere 10, 100, 1000 eller et hvilket som helst tall som er basis 10
Dette kan være en enkel måte å konvertere brøk til desimaler uten å bruke lang divisjon eller en kalkulator. Finn først et tall som kan multipliseres med brøkets nevner for å få 10, 100, 1000, og så videre. For å gjøre dette, del først 10, deretter 100, deretter 1000, og så videre med nevneren til du får et helt tall. Eksempel:
- 3/5. 10/5 = 2.2 er et helt tall. 2 kan multipliseres med 5 for å gjøre 10. Så kan 2 brukes.
- 3/4. 10/4 = 2, 5. 2, 5 er ikke et helt tall. 100/4 = 25. 25 er et helt tall. 25 kan multipliseres med 4 for å gjøre 100. Så 25 kan brukes.
- 16.5. 10/16 = 0, 625, 100/16 = 6, 25, 1000/16 = 62, 5, 10.000/16 = 625. 625 er det første heltallet som oppnås. 625 kan multipliseres med 16 for å få 10 000. Så, 625 kan brukes.
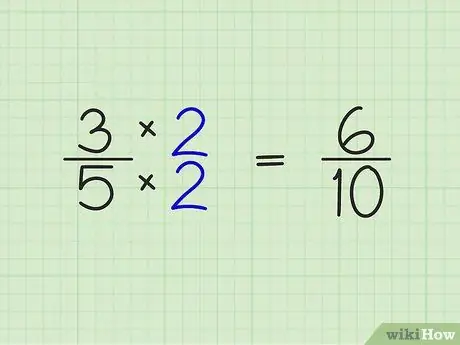
Trinn 2. Multipliser telleren og nevneren til brøkdelen med hele tallet som ble oppnådd fra forrige trinn
Dette trinnet er ganske enkelt. Bare multipliser tallene over og under brøkdelen med hele tallet du fikk i forrige trinn. Eksempel:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3.125/10000

Trinn 3. Skriv det endelige svaret
Svaret er at telleren er markert med en desimal i henhold til tallet 0 i nevneren. Bare tell hvor mange 0 -er som er i nevneren. Hvis det bare er 1 0 i nevneren, flytter du desimaltegnet til venstre med 1 siffer, og så videre. Eksempel:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Metode 4 av 4: Med kalkulator

Trinn 1. Del telleren med nevneren
Denne metoden er veldig enkel. Bare bruk en kalkulator for å dele telleren, tallet øverst i brøken, med nevneren, tallet nederst i brøken. For eksempel, si at du vil konvertere 3/4 til en desimal. Bare trykk "3", deretter divisjonssymbolet ("÷ '"), deretter "4", og til slutt likesymbolet ("=").

Trinn 2. Skriv ned svarene du får
Svaret er 0,75. Så desimalformen til den felles brøk 3/4 er 0,75.
Tips
- For å sjekke om svaret ditt er riktig, multipliser du svaret med nevneren til brøken. Hvis svaret ditt er riktig, er produktet av multiplikasjonen telleren av brøken.
- Noen brøk kan konverteres til desimaler ved å lage sammenlignbare brøker hvis nevnere er basis 10 (10, 100, 1000 og så videre). Deretter bruker du stedsverdier til å skrive ned riktig desimalform.






