For de fleste er brøk de første kompliserte beregningene som kommer over. Begrepet fraksjoner er ganske vanskelig og krever at du lærer spesielle forhold for å gjøre det. Fordi brøk har spesielle regler for addisjon, subtraksjon, multiplikasjon og divisjon, er mange mennesker forvirret om det. Men med mye øvelse kan hvem som helst lære og fullføre beregninger knyttet til brøk.
Steg
Metode 1 av 5: Forstå fraksjoner
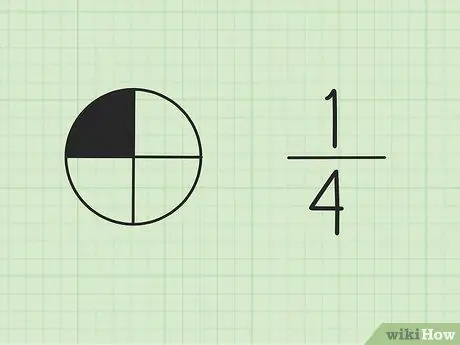
Trinn 1. Forstå at brøkdeler er en del av en helhet
Tallet øverst kalles teller, og representerer antall deler av totalen. Tallet nederst kalles nevner, som representerer det totale antall deler.
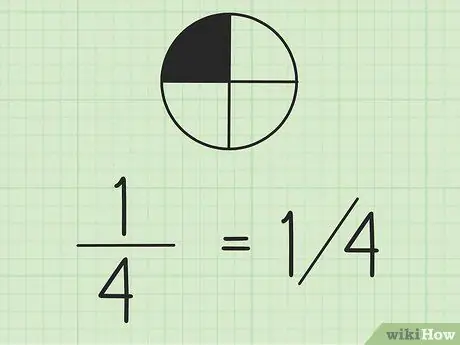
Trinn 2. Husk at du kan skrive brøk ved å bruke skråstreker
Tallet til venstre er telleren og tallet til høyre er nevneren. Hvis du jobber med brøk på samme linje, er det en god idé å skrive telleren over nevneren.
For eksempel, hvis du tar en av fire pizzaskiver, har du pizza. Hvis du har 7/3 pizzaer, betyr det at du har to hele pizzaer pluss 1 av 3 pizzaskiver
Metode 2 av 5: Forskjell mellom blandede og enkle fraksjoner
Trinn 1. Forstå at blandede tall består av hele tall og brøk, for eksempel 2 1/3 eller 45 1/2
Vanligvis må du konvertere blandede tall til en enklere form for å legge til, trekke fra, multiplisere eller dele.
Trinn 2. Endre det blandede tallet ved å multiplisere hele tallet med nevneren i brøken, og deretter legge det til med telleren
Skriv resultatet som teller, mens nevneren ikke endres.
For eksempel, for å konvertere 2 1/3 til en enkel brøk, multipliser 2 med 3, legg deretter til 1 og få 7/3
Trinn 3. Konverter enkle brøker til blandede tall ved å dele telleren med nevneren
Hele resultatet av divisjonen skrives som et heltall, og resten av divisjonen skrives som telleren av brøken. Nevneren endres ikke.
For eksempel, for å konvertere 7/3 til et blandet tall, dividerer 7 med 3 for å få 2 med resten av 1. Så det blandede tallet er 2 1/3. Enkle brøk kan bare konverteres til blandede tall hvis telleren er større enn nevneren
Metode 3 av 5: Addisjon og subtraksjon av fraksjoner
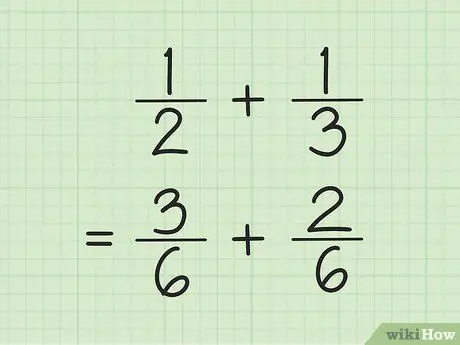
Trinn 1. Finn en fellesnevner for å legge til og trekke fraksjoner
Trikset, multipliser tallene i nevneren, og multipliser deretter hver teller med tallet som brukes til å finne nevneren. Noen ganger kan du finne LCM (minst felles multiplum) for nevneren ved å multiplisere nevnerne med hverandre.
For eksempel, for å legge til og 1/3, må du først finne LCM (minst felles multiplum) av de to nevnerne ved å multiplisere hverandre. Dermed multipliserer du 2 og 3 for å få LCM 6. Multipliser 1 med 3 for å få 3 som den nye telleren til den første brøkdelen. Multipliser 1 med 2 for å få 2 som den nye telleren til den andre brøkdelen. De nye brøkene er 3/6 og 2/6
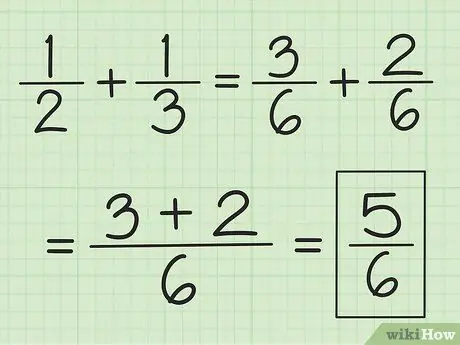
Trinn 2. Legg de to tellerne sammen og ikke endre nevneren
For eksempel er 3/6 pluss 2/6 5/6, og 2/6 pluss 1/6 er 3/6
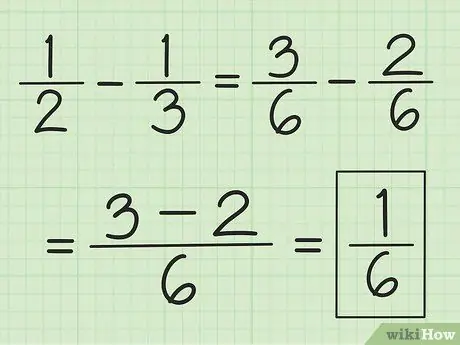
Trinn 3. Bruk en lignende teknikk for subtraksjon
Finn LCM for nevnerne først, men i stedet for å legge dem sammen, trekker du nummeret til den første telleren med nummeret til den andre.
For eksempel, for å trekke 1/3 fra 1/2, endrer du først brøkene til 3/6 og 2/6, deretter trekker du 3 av 2 for å få 1. Dette resulterer i 1/6
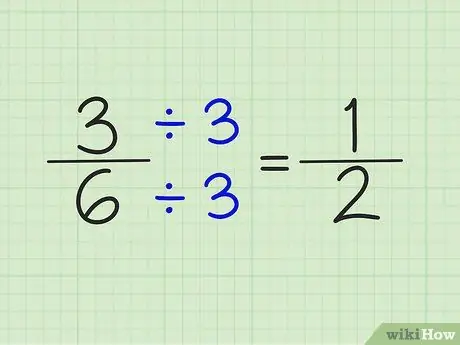
Trinn 4. Forenkle brøk ved å dele teller og nevner med samme tall
For eksempel kan tallet 5/6 ikke forenkles. Imidlertid kan 3/6 forenkles ved å dele teller og nevner med tallet 3. Resultatet er en brøkdel av 1/2
Trinn 5. Konverter brøkdelen til et blandet tall hvis telleren er større enn nevneren
Metode 4 av 5: Multiplisere og dele fraksjoner
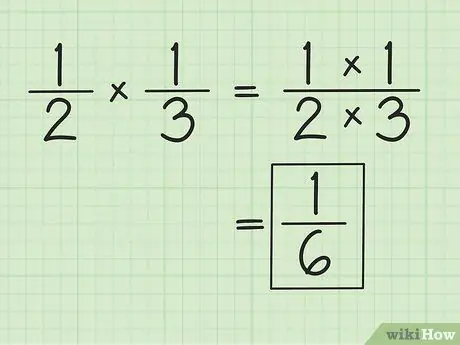
Trinn 1. Multipliser teller og nevner separat for å multiplisere brøker
For eksempel, når du multipliserer og 1/3, er resultatet 1/6 (1 ganger 1 og 2 ganger 3). Du trenger ikke å matche nevnerne når du multipliserer brøk. Forenkle eller endre resultatene som er oppnådd, om nødvendig
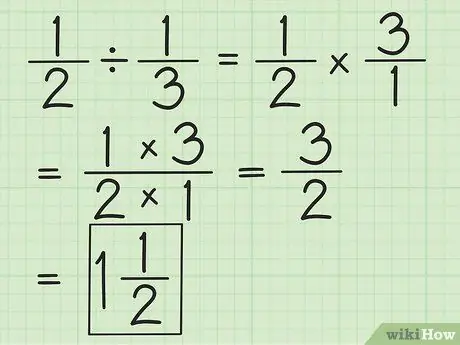
Trinn 2. Del to fraksjoner ved å snu den andre fraksjonen, og multipliser deretter begge
For eksempel, hvis du vil dele 1/2 med 1/3, snu først den andre fraksjonen til 3/1. Multipliser med 3/1 og få 3/2. Forenkle brøk eller konverter om mulig til blandede tall
Metode 5 av 5: Arbeide med komplekse fraksjoner
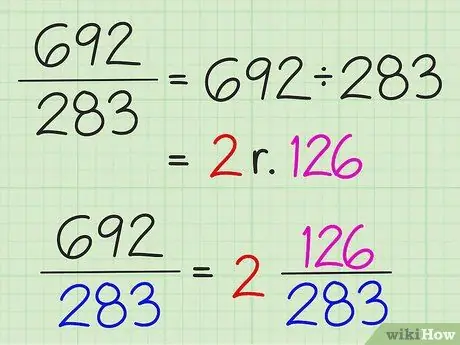
Trinn 1. Arbeid alle brøkene på samme måte, selv om problemet virker veldig komplisert
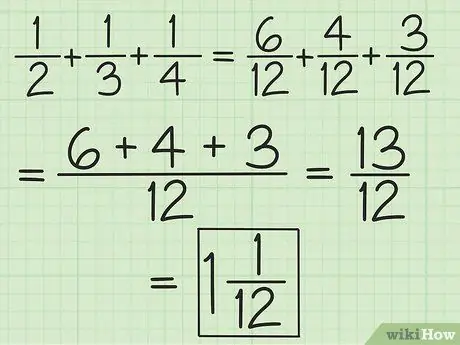
Trinn 2. Match nevnerne for alle brøkene eller arbeid i par fra venstre til høyre for å legge til og trekke fra mer enn to brøk
For eksempel, for å legge opp 1/2, 1/3 og 1/4, kan du endre dem til 6/12, 4/12 og 3/12 for å få 13/12, eller du kan legge til 3/6 og 2 /6 så får du 5/6, legg deretter til 5/6 og 1/4 (utlign nevnerne slik at den andre brøkdelen blir 3/12) for å få 13/12 (10/12 pluss 3/12). Konverter det til et blandet tall, som er 1 1/12
Tips
- Husk at du har lært ganske mye matte. Matematikk er som et språk du kan uttale flytende, og nå prøver du å lære å lese og skrive det.
- Husk å alltid forenkle det endelige resultatet av beregningen, enten problemet ditt er i form av en vanlig brøk, et blandet tall eller en kompleks brøk.
