Med Spearmans rangekorrelasjonskoeffisient kan vi identifisere om to variabler har et monoton funksjonsforhold (det vil si at når det ene tallet øker, vil det andre tallet også øke, eller omvendt). For å beregne Spearmans rangekorrelasjonskoeffisient, må du rangere og sammenligne datasett for å finne d2, og skriv deretter inn dataene i standard eller forenklet Spearman -rangekorrelasjonskoeffisientformel. Du kan også beregne disse koeffisientene ved hjelp av Excel -formler eller R -kommandoen.
Steg
Metode 1 av 3: Manuell måte
Trinn 1. Lag et bord
Tabellen brukes til å inkludere all informasjonen som trengs for å beregne Spearman Rank -korrelasjonskoeffisienten. Du trenger et bord som dette:
- Lag 6 kolonner med overskrifter, som i eksemplet.
- Forbered så mange blanke rader som antall datapar.
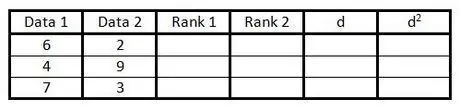
Trinn 2. Fyll ut de to første kolonnene med datapar
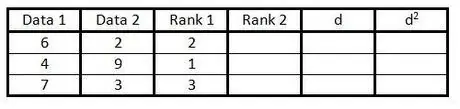
Trinn 3. Angi rangeringen av den første kolonnen med datagrupper i den tredje kolonnen fra 1 til n (antall data)
Gi en vurdering på 1 for den laveste verdien, en vurdering på 2 for den neste laveste verdien, og så videre.
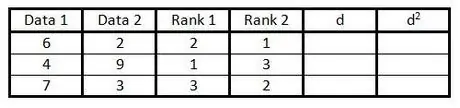
Trinn 4. Gjør det samme som i trinn 3 i den fjerde kolonnen, men for å rangere dataene i den andre kolonnen
-
Gjennomsnitt_742 Hvis det er to (eller flere) data som har samme verdi, beregner du gjennomsnittlig vurdering av dataene, og skriver dem deretter inn i en tabell basert på denne gjennomsnittlige verdien.
I eksemplet til høyre er det to verdier på 5 på vurderingene 2 og 3. Siden det er to 5 -er, finn gjennomsnittet av vurderingene. Gjennomsnittet på 2 og 3 er 2,5, så skriv inn en vurderingsverdi på 2,5 for begge verdiene 5.
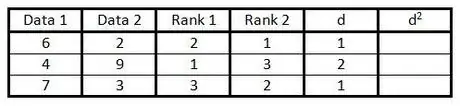
Trinn 5. I kolonne "d" beregner du forskjellen mellom de to tallene i rangekolonnen
Det vil si at hvis en kolonne er rangert 1 og den andre kolonnen er rangert 3, er forskjellen 2. (Tegnet spiller ingen rolle, fordi neste trinn er å kvadrere verdien.)
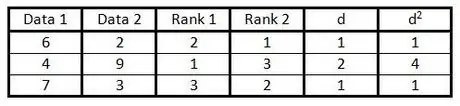
Trinn 6. Kvadrater hvert tall i kolonne "d" og skriv resultatet i kolonne "d2".
Trinn 7. Legg til alle dataene i kolonne d2".
Resultatet er d2.
Trinn 8. Velg en av følgende formler:
-
Hvis ingen av vurderingene er de samme som i forrige trinn, angir du denne verdien i den forenklede formelen for Spearman Rank Correlation Coefficient
Trinn 8_271 og erstatt "n" med antall datapar for å få resultatet.
Trinn 9_402 -
Hvis det er en lignende rangering i forrige trinn, bruker du standardformelen for Spearman Rank Correlation Coefficient:
Spearman
Trinn 9. Tolk resultatene
Verdien kan variere mellom -1 og 1.
- Hvis verdien er nær -1, er korrelasjonen negativ.
- Hvis verdien er nær 0, er det ingen lineær korrelasjon.
- Hvis verdien er nær 1, er korrelasjonen positiv.
Metode 2 av 3: Bruke Excel
Trinn 1. Lag en ny kolonne for dataene sammen med rangeringen
For eksempel, hvis dataene dine er i kolonne A2: A11, bruk formelen "= RANK (A2, A $ 2: A $ 11)", og kopier den ned til den dekker alle kolonnene og radene.
Trinn 2. Endre samme vurdering som beskrevet i trinn 3 og 4 i metode 1
Trinn 3. I den nye cellen beregner du korrelasjonen mellom de to rangkolonnene med formelen "= CORREL (C2: C11, D2: D11)"
I dette eksemplet refererer C og D til kolonnen der rangeringen er plassert. Den nye cellen vil bli fylt med Spearman Rank Correlation.
Metode 3 av 3: Bruke R
Trinn 1. Installer R -programmet først hvis du ikke allerede har det
(Se
Trinn 2. Lagre dataene dine i CSV -skjema, legg dataene du vil finne korrelasjonen i de to første kolonnene
Vi kan gjøre dette ved å bruke "Lagre som" -menyen.
Trinn 3. Åpne R Editor
Hvis du jobber fra terminalen, bare kjør R. Hvis du jobber fra skrivebordet, klikker du på ikonet R.
Trinn 4. Skriv inn følgende kommando:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") og trykk Enter.
- cast (rang (d [, 1]), rang (d [, 2]))
Tips
Dataene må bestå av minst 5 par slik at trenden kan sees (antall data er 3 par i eksemplet bare for å forenkle beregninger.)
Advarsel
- Korrelasjonskoeffisienten for Spearman -rang identifiserer bare styrken til korrelasjonen der dataene stiger eller faller konsekvent. Hvis det er en annen trend i dataene, Spearmans rangekorrelasjon Nei vil gi en nøyaktig fremstilling.
- Denne formelen er basert på antagelsen om at det ikke er like vurderinger. Når det er samme rang som i eksemplet, bør vi bruke denne definisjonen: korrelasjonskoeffisienten til multiplikasjonsmomentet etter rang.
