Det kan virke skremmende å finne antall termer i en aritmetisk serie, men det er faktisk ganske enkelt. Du trenger bare å skrive inn tallene i formelen U = a + (n - 1) b og finn verdien av n, som er antall termer. Vet at U er det siste tallet i serien, a er det første uttrykket i serien, og b er forskjellen mellom tilstøtende termer.
Steg
Trinn 1. Identifiser det første, andre og siste uttrykket i serien
Vanligvis gir spørsmål som dette de første 3 eller flere vilkårene, og det siste uttrykket.
Anta for eksempel at spørsmålet ditt er slik: 107, 101, 95 … -61. I dette tilfellet er den første termen 107 og den siste termen er -61. Du trenger all denne informasjonen for å løse problemet
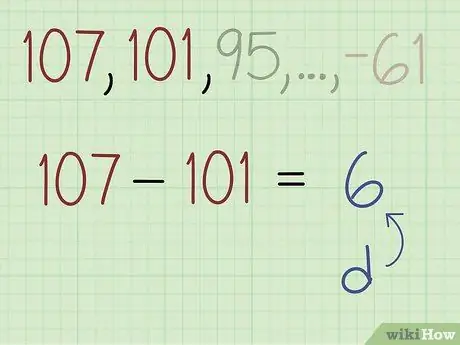
Trinn 2. Trekk det andre uttrykket fra det første uttrykket for å finne forskjellen (b)
I eksempelproblemet er det første uttrykket 107 og det andre uttrykket er 101. For å finne forskjellen, trekker du 101 med 107 og får -6.
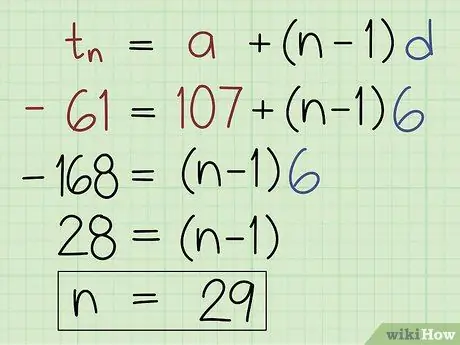
Trinn 3. Bruk formelen U = a + (n - 1) b for å finne n.
Skriv inn den siste termen (U ), det første uttrykket (a) og forskjellen (b). Telle ligningene til du får verdien av n.
