- Forfatter Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Sist endret 2025-01-23 12:42.
Subtraksjon er ganske enkelt å trekke ett tall fra et annet. Det er lett å trekke et helt tall fra et annet, men subtraksjon kan være vanskelig hvis du trekker fra brøk eller desimaler. Når du forstår subtraksjon, vil du kunne bruke mer komplekse matematiske begreper, og lettere kunne legge til, multiplisere og dele tall.
Steg
Metode 1 av 6: Trekker fra store tall ved å låne

Trinn 1. Skriv ned et stort antall
For eksempel vil du løse 32 - 17. Skriv ned 32 først.

Trinn 2. Skriv det mindre tallet rett under det
Sørg for at du plasserer tiene og enene verdiene i de riktige kolonnene, slik at 3 av 32 er rett over 1 av 17 og 2 av 32 er rett over 7 av 17.
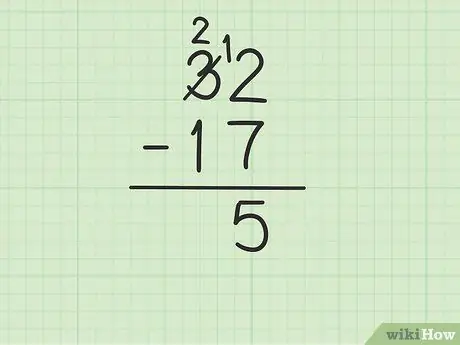
Trinn 3. Trekk det øverste tallet i enhetskolonnen fra tallet nederst
Dette kan imidlertid bli komplisert hvis det nederste tallet er større enn det øverste tallet. I dette tilfellet er 7 større enn 2. Her er det du må gjøre:
- Du må låne fra nummer 3 på 32 (også kjent som gruppering), for å gjøre 2 til 12.
- Kryss tallet 3 av 32 og erstatt det med tallet 2, mens tallet 2 blir 12.
- Nå kan du trekke fra 12 - 7, som tilsvarer 5. Skriv 5 under de to tallene du trekker fra, slik at de er i enhetskolonnen i den nye raden.
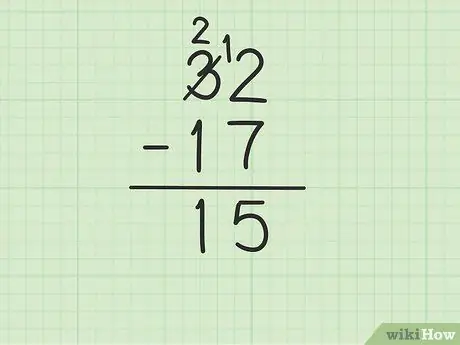
Trinn 4. Trekk det øverste tallet i tienskolonnen fra det nederste tallet
Husk 3 har blitt 2. Trekk nå 1 fra 17 fra 2 ovenfor for å få (2-1) 1. Skriv 1 nedenfor, i tienskolonnen, til venstre for 5 i enhetskolonnen. Du skriver 15. Det vil si 32 - 17 = 15.
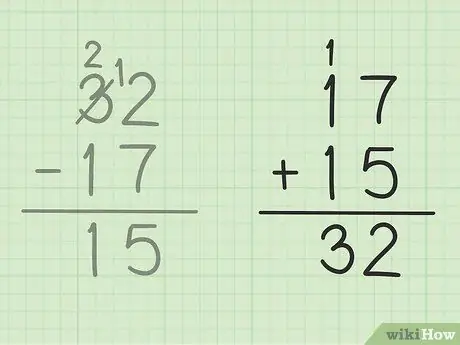
Trinn 5. Sjekk arbeidet ditt
Hvis du vil være sikker på at du har trukket fra to tall riktig, er det bare å legge opp svaret ditt med det mindre tallet for å lage et stort tall. I dette problemet må du legge svaret ditt, 15 til det mindre antallet subtraksjon, 17. 15 + 17 = 32, slik at svaret ditt er riktig. Sikker!
Metode 2 av 6: Trekk fra små tall
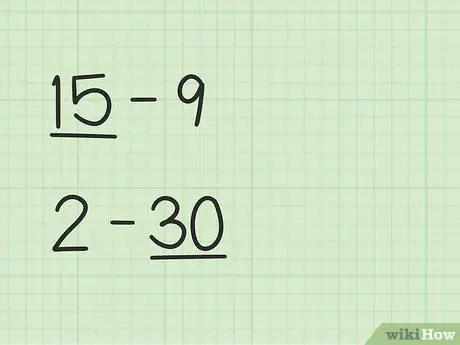
Trinn 1. Finn det større tallet
Problemer som 15 -9 vil ha en annen måte enn 2 -30.
- I spørsmål 15 - 9 er det første tallet, 15, større enn det andre tallet, 9.
- I spørsmål 2 - 30 er det andre tallet, 30, større enn det første tallet, 2.
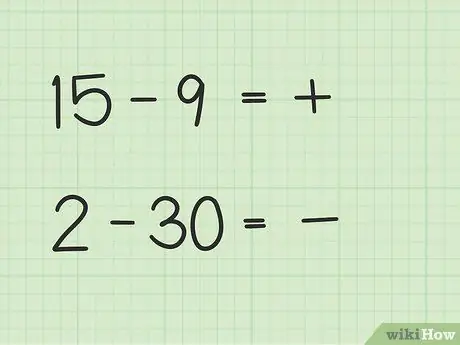
Trinn 2. Bestem om svaret ditt vil være positivt eller negativt
Hvis det første tallet er større, er svaret positivt. Hvis det andre tallet er større, er svaret negativt.
- I det første spørsmålet, 15 - 9, er svaret positivt fordi det første tallet er større enn det andre tallet.
- I det andre spørsmålet, 2 - 30, er svaret ditt negativt fordi det andre tallet er større enn det første tallet.
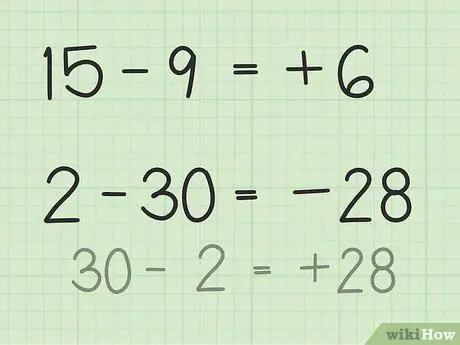
Trinn 3. Finn forskjellen mellom to tall
For å trekke fra to tall, må du forestille deg forskjellen mellom de to tallene og beregne tallene mellom dem.
- For spørsmål 15 - 9, tenk deg en bunke med 15 pokerbrikker. Kast 9 sjetonger og bare 6. Så, 15 - 9 = 6. Du kan også forestille deg en tallinje. Tenk på tallene fra 1 til 15, og kast eller returner 9 enheter, slik at du får 6.
- For spørsmål 2 - 30 er den enkleste måten å løse dette på å invertere tallet og gjøre resultatet negativt etter å ha trukket fra. Så, 30 - 2 = 28 så 28 og 30 har en forskjell på 2. Gjør nå resultatet negativt fordi du allerede har bestemt at svaret er negativt fordi det andre tallet er større enn det første tallet. Så, 2 -30 = -28.
Metode 3 av 6: Trekker fra desimaler
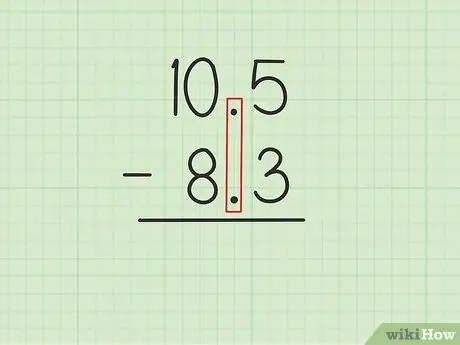
Trinn 1. Skriv det større tallet over det mindre tallet med desimalpunktene justert
Anta at du vil løse følgende problemer: 10, 5 - 8, 3. Skriv 10, 5 over 8, 3 slik at desimalpunktene til de to tallene er parallelle., 5 av 10, 5 må være rett over, 3 av 8, 3 og 0 av 10, 5 må være over 8 av 8, 3.
Hvis du har et problem fordi de to tallene ikke har samme tall etter desimaltegnet, skriver du 0 i feltet til summen av tallene er den samme. For eksempel er problemet 5, 32 - 4, 2, du kan skrive det som 5, 32 - 4, 2 0. Dette vil ikke endre verdien til det andre tallet, men det vil gjøre det lettere å trekke fra de to tallene.

Trinn 2. Trekk det øverste tallet i tienskolonnen fra tallet nedenfor
I dette tilfellet må du trekke 3 fra 5. 5 - 3 = 2, så du må skrive 2 under 3 av 8, 3.
Sørg for å sette et desimaltegn i svaret, slik at det skrives, 2

Trinn 3. Trekk tallet over kolonnen enheter fra tallet under det
Du må trekke 8 fra 0. Lån 1 fra tiendelen for å endre 0 til 10 og trekke fra 10 - 8 for å få 2. Du kan også telle 10 - 8 uten å låne fordi det ikke er tall i den andre tierkolonnen. Skriv svaret under 8, til venstre for desimaltegnet.

Trinn 4. Skriv ned det endelige resultatet
Det endelige resultatet er 2, 2.

Trinn 5. Sjekk arbeidet ditt
Hvis du vil sørge for at din desimale subtraksjon er riktig, er alt du trenger å gjøre å legge opp svaret ditt med det mindre tallet for å få det større tallet. 2, 2 + 8, 3 = 10, 5, så du er ferdig.
Metode 4 av 6: Trekk fraksjoner

Trinn 1. Juster nevneren og telleren for brøkdelen
Anta at du vil løse problemer 13/10 - 3/5. Skriv oppgaven slik at de to tellerne 13 og 3 og de to nevnerne 10 og 5 står overfor hverandre. Disse to tallene er atskilt med et subtraksjonstegn. Dette vil hjelpe deg med å visualisere problemet og løse det lettere.

Trinn 2. Finn den minst fellesnevner
Den minst fellesnevner er det minste tallet som kan deles med to tall. I dette eksemplet må du finne den minste fellesnevner som er delelig med 10 og 5. Du vil finne at 10 er den minste fellesnevner for begge tallene fordi 10 er delelig med 10 og 5.
Vær oppmerksom på at den minst felles nevneren av to tall ikke alltid er ett av dem. For eksempel er den minste fellesnevner for 3 og 2 6 fordi 6 er det minste tallet som kan deles med to tall
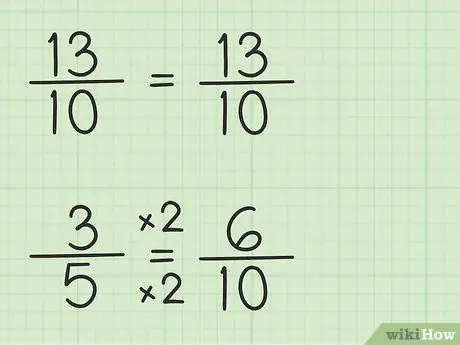
Trinn 3. Skriv ned brøkene ved å bruke samme nevner
Brøk 13/10 kan skrives på samme måte fordi nevneren er 10, den minste fellesnevner, som er 10, ganger 1. Imidlertid må brøkdelen 3/5 skrives om fordi nevneren er 5, den minste fellesnevner, som er 10, ganger 2. Så brøkdelen 3/5 må multipliseres med 2/2 for å gjøre nevneren 10, så 3/5 x 2/2 = 6/10. Du har funnet tilsvarende brøk. 3/5 tilsvarer 6/10, selv om 6/10 lar deg trekke fra det første tallet, 13/10.
Skriv et nytt spørsmål som dette: 13/10 - 6/10
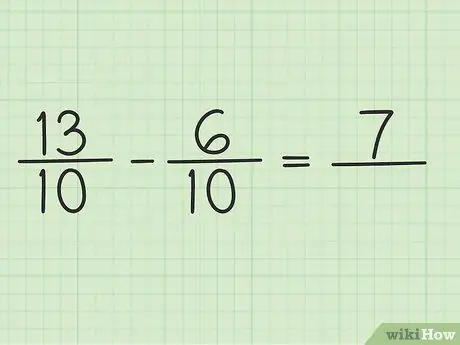
Trinn 4. Trekk telleren til to tall
Bare trekk fra 13 - 6 så blir resultatet 7. Du kan ikke endre nevneren til brøken.
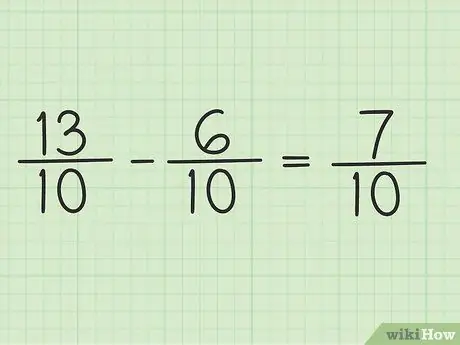
Trinn 5. Skriv den nye telleren over samme nevner for å få det endelige resultatet
Den nye telleren er 7. Begge brøkene har en nevner på 10. Det endelige resultatet er 7/10.
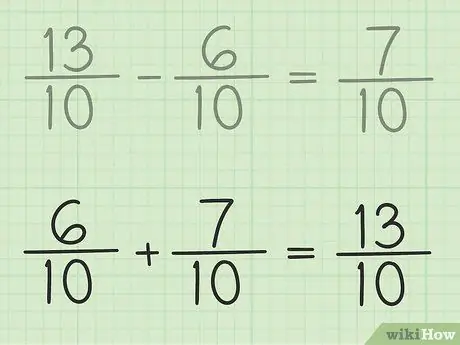
Trinn 6. Sjekk arbeidet ditt
Hvis du vil være sikker på at du trekker fraksjonen riktig, legger du bare sammen svaret ditt og den mindre brøkdelen slik at resultatet blir en større brøk. 7/10 + 6/10 = 13/10. Det er ferdig.
Metode 5 av 6: Trekker fraksjoner fra hele tall

Trinn 1. Skriv ned problemet
Anta for eksempel at du vil løse følgende problem: 5 -. Skriv det ned.
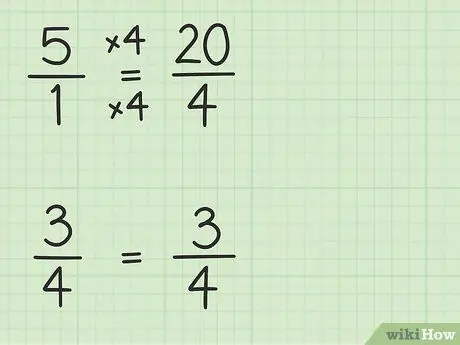
Trinn 2. Konverter hele tall til brøk som har samme nevner som andre brøk
Du vil konvertere 5 til en brøk med en nevner på 4 for å kunne trekke to tall. Så du må tenke på 5 som en brøkdel av 5/1. Deretter kan du multiplisere den nye brøkets teller og nevner med 4 for å gjøre de to tallenes nevnere like. Så 5/1 x 4/4 = 20/4. Denne brøkdelen er lik 5, men lar deg trekke fra to tall.
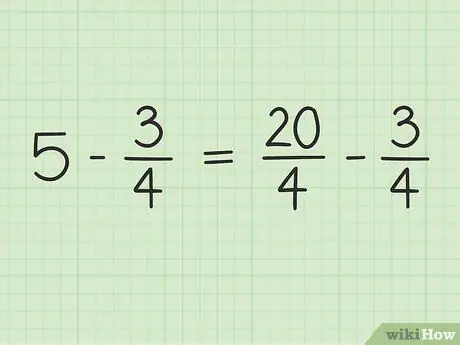
Trinn 3. Skriv om problemet
Det nye problemet kan skrives slik: 20/4 - 3/4.
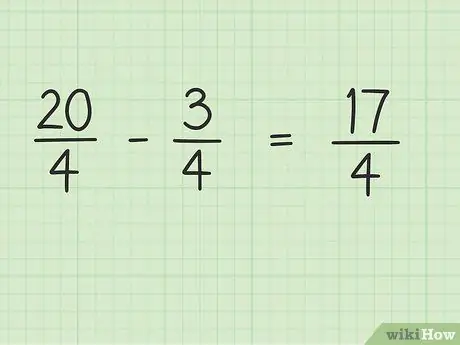
Trinn 4. Trekk telleren til brøkdelen, mens nevneren forblir den samme
Nå er det bare å trekke fra 20 x 3 for å få det endelige resultatet. 20 - 3 = 17, så 17 er den nye telleren. Du kan la nevneren være den samme.
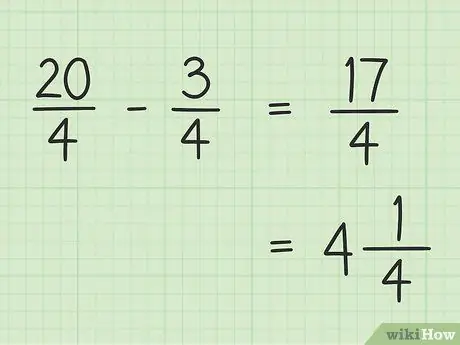
Trinn 5. Skriv ned det endelige resultatet
Det endelige resultatet ditt er 17/4. Hvis du vil skrive det som et blandet tall, deler du 17 med 4 slik at resultatet er 4 og resten er 1, slik at den siste 17/4 er lik 4.
Metode 6 av 6: Trekke fra variabler
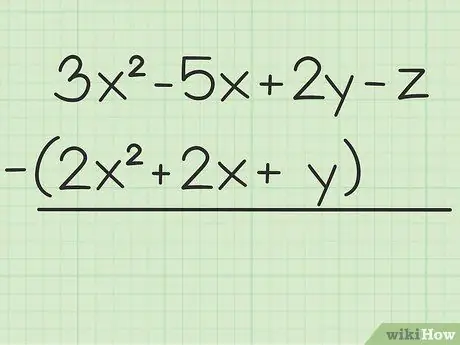
Trinn 1. Skriv ned problemet du vil løse
For eksempel følgende spørsmål: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Skriv det første settet med variabler over det andre.
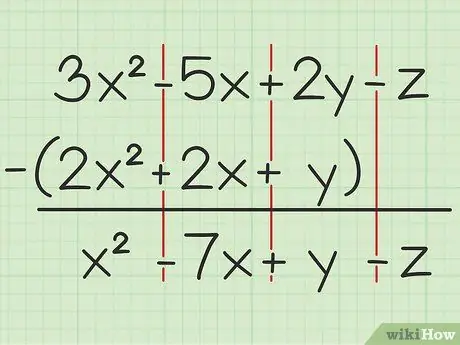
Trinn 2. Trekk fra de samme variablene
Hvis du støter på en variabel, kan du bare legge til eller trekke fra den samme variabelen og som er skrevet med samme grad av kvadrat. Det betyr at du kan trekke fra 4x2 fra 7x2, men kan ikke trekke 4x fra 4y. Så du kan dele problemet slik:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
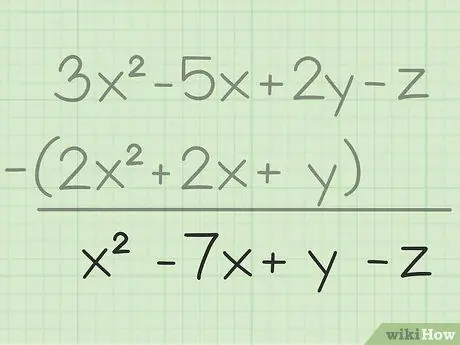
Trinn 3. Skriv ned det endelige resultatet
Du har trukket fra alle de samme variablene, alt du trenger å gjøre er å skrive det endelige resultatet som vil inneholde alle variablene du har trukket fra. Her er sluttresultatet:






