- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:21.
- Sist endret 2025-01-23 12:42.
Å legge til og trekke fraksjoner er en viktig ferdighet å ha. Brøk dukker opp i hverdagen hele tiden, spesielt i matematikkundervisning, fra grunnskolen til høyskolen. Følg disse trinnene for å lære hvordan du legger til og trekker brøk, fra ekvivalente brøker, ulik brøk, blandede tall eller vanlige brøker. Hvis du allerede vet en måte, er det veldig enkelt å løse de andre brøkene!
Steg
Metode 1 av 4: Legge til og trekke fra brøk med samme nevner
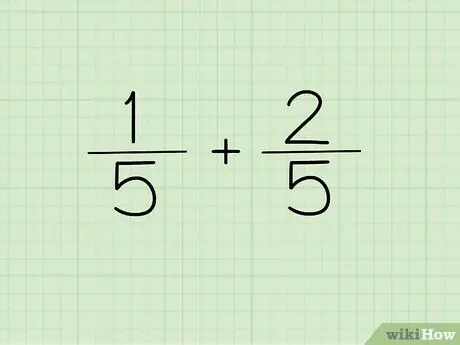
Trinn 1. Skriv ned spørsmålet ditt
Hvis nevneren til de to brøkene du vil legge til eller trekke fra er den samme, skriver du nevneren en gang som nevner for svaret ditt.
Med andre ord trenger ikke 1/5 og 2/5 skrives som 1/5 + 2/5 =?, men kan skrives som (1+2)/5 =?. Nevnerne er de samme, så de kan bare skrives en gang. De to tellerne kombineres
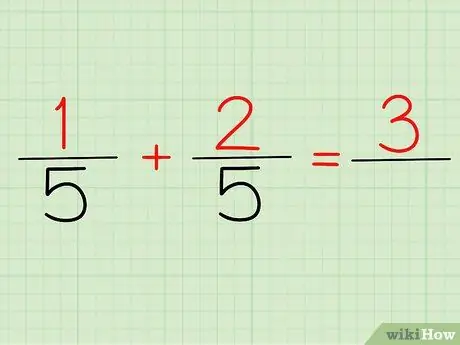
Trinn 2. Legg opp tellerne
Telleren er tallet som er over enhver brøk. Hvis vi ser på problemet ovenfor, er 1/5 og 2/5, 1 og 2 våre tellere.
Enten du skriver det 1/5 + 2/5 eller (1 + 2)/5, vil svaret ditt være det samme: 3! Fordi 1 + 2 = 3

Trinn 3. La nevneren stå
Siden nevnerne er de samme, ikke gjør noe med nevnerne! Ikke legg til, trekk fra, multipliser eller del. La det være.
Så, fra samme eksempel, er nevneren vår 5. Høyre! 5 er det nederste tallet i vår brøk. Vi har halve svaret

Trinn 4. Skriv ned svaret ditt
Alt du trenger å gjøre er å skrive ned telleren og nevneren! Hvis du bruker eksemplet ovenfor, vil svaret ditt være 3/5.
Hva er telleren din? 3. Din nevner? 5. Derfor er 1/5 + 2/5 eller (1 + 2)/5 lik 3/5.
Metode 2 av 4: Addisjon og subtraksjon av brøker med forskjellige nevnere

Trinn 1. Finn den minst felles nevneren
Det vil si at den minste nevneren er den samme for begge brøkene. Anta at vi har brøkene 2/3 og 3/4. Hva er nevneren? 3 og 4. For å finne den minst felles nevneren for begge brøkene, kan du gjøre dette på tre måter:
- Skriv ned multipler av. Multipler av 3 er 3, 6, 9, 12, 15, 18 … og så videre. Multipler på 4? 4, 8, 12, 16, 20, og så videre. Hva er det minste tallet som er et multiplum av de to? 12! Det er den minst fellesnevner.
-
Primtallsfaktorisering. Hvis du vet om faktorer, kan du gjøre primfaktorisering. Det vil si at du leter etter tallene som utgjør din nevner. For tallet 3 er faktorene 3 og 1. For tallet 4 er faktorene 2 og 2. Deretter alle sammen. 3 x 2 x 2 = 12. Din minst fellesnevner!
Multipliser alle tallene for det mindre tallet. I noen problemer, som denne, kan du multiplisere begge tall - 3 x 4 = 12. Men hvis du har en stor nevner, ikke gjør dette! Du vil ikke multiplisere 56 x 44 og gå alt for å få 2464

Trinn 2. Multipliser nevneren med tallet som trengs for å få den minste fellesnevneren
Med andre ord vil du at alle nevnerne skal være like. I vårt eksempel vil vi at nevneren skal være 12. For å endre 3 til 12, multipliserer du 3 med 4. For å endre 4 til 12, multipliserer du 4 med 3. Den samme nevneren vil være nevneren for det endelige svaret ditt.
-
Så 2/3 blir 2/3 x 4 og 3/4 blir 3/4 x 3. Det vil si at vi nå har 2/12 og 3/12. Men, vi er ikke ferdige ennå!
- Du vil legge merke til at nevnerne multipliseres med hverandre. Dette kan gjøres i denne situasjonen, men ikke i alle situasjoner. Noen ganger, i stedet for å multiplisere begge nevnerne, kan du multiplisere begge nevnerne med et annet tall for å få det mindre tallet.
- I andre problemer trenger du noen ganger bare å multiplisere den ene nevneren for å gjøre den lik nevneren til den andre fraksjonen i problemet.

Trinn 3. Multipliser telleren med det samme tallet
Når du multipliserer nevneren med et tall, må du også multiplisere telleren med det samme tallet. Det vi gjorde i det siste trinnet er bare en del av multiplikasjonen som må gjøres.
Vi har 2/3x4 og 2/4x3 som det første trinnet - deretter, i det andre trinnet, 2 x 4/3 x 4 og 3 x 3/4 x 3. Det vil si at våre nye tall er 8/12 og 9/ 12. Perfekt
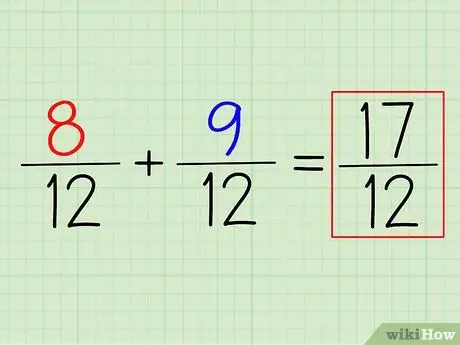
Trinn 4. Legg til (eller trekk fra) tellerne for å få svaret
For å legge til 8/12 + 9/12, er det bare å legge opp tellerne. Husk: bare la nevneren stå. Den minste fellesnevneren du finner er den siste nevneren.
I dette eksemplet, (8+9)/12 = 17/12. For å konvertere det til et blandet tall, trekker du bare nevneren fra telleren og skriver ned resten. I dette tilfellet er 17/12 = 1 5/12
Metode 3 av 4: Addisjon og subtraksjon av blandede og vanlige fraksjoner
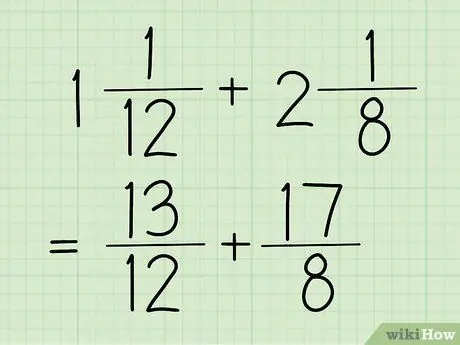
Trinn 1. Konverter dine blandede fraksjoner til vanlige fraksjoner
Et blandet tall er en brøk som har et helt tall og en brøk, som i eksemplet ovenfor (1 5/12). I mellomtiden er en vanlig brøkdel en brøk hvis teller (toppnummer) er større enn nevneren (nederste tall). Denne brøkdelen er også sett i forrige trinn, som er 17/12.
For eksemplene i denne delen vil vi bruke 13/12 og 17/8

Trinn 2. Finn en fellesnevner
Husker du de tre måtene å finne den minst felles nevneren? Ved å skrive multipler, bruke primfaktorisering eller multiplisere nevnerne.
La oss finne flere av eksemplet vårt, 12 og 8. Hva er det minste tallet som begge har til felles? 24. 8, 16, 24 og 12, 24 - bingo

Trinn 3. Multipliser telleren og nevneren for å finne tilsvarende brøk
Begge nevnerne må endres til 24. Hvordan konverterer du 12 til 24? Multipliser med 2. 8 til 24? Multipliser med tre. Men ikke glem - du må multiplisere tellerne også!
Så (13 x 2)/(12 x 2) = 26/24. Og (17 x 3)/(8 x 3) = 51/24. Vi er nesten ferdige med dette

Trinn 4. Legg til eller trekk fra brøkene dine
Nå som du har samme nevner, kan du enkelt legge de to tellerne sammen. Husk, bare la nevneren stå!
26/24 + 51/24 = 77/24. Det er summen din! Tallene på toppen var imidlertid for store …

Trinn 5. Konverter svaret ditt tilbake til blandede tall
Det veldig store tallet øverst i brøkdelen føles litt rart - du kan ikke se størrelsen på brøkdelen din. Alt du trenger å gjøre er å trekke nevneren fra telleren gjentatte ganger til den ikke kan trekkes videre og skrive ned resten.
-
I dette eksemplet, 77 minus 24 ganger 3 ganger. Det vil si 24 x 3 = 72. Resten er 5! Så hva er sluttresultatet ditt? 3 5/24.
Så sant!
Metode 4 av 4: Legg til og trekk fraksjoner uten å finne LCM
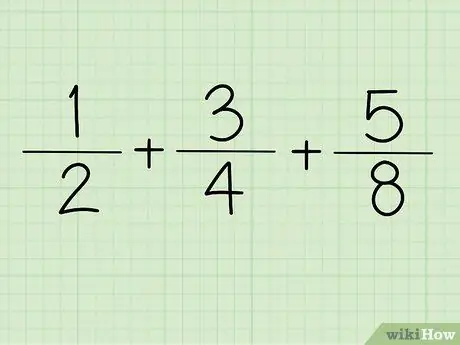
Trinn 1. Skriv ned brøkdelen
For eksempel + +

Trinn 2. Løs telleren først
- Multipliser med den andre brøkens teller.
- Multipliser 1 med 4 og 8. [32]
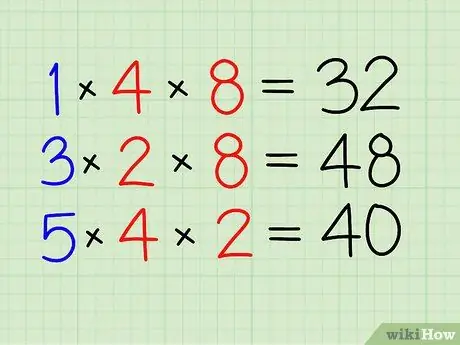
Trinn 3. Gjør det samme for de andre fraksjonene
- Multipliser 3 med 2 og 8. [48]
- Til slutt multipliserer du 5 med 4 og 2. [40]
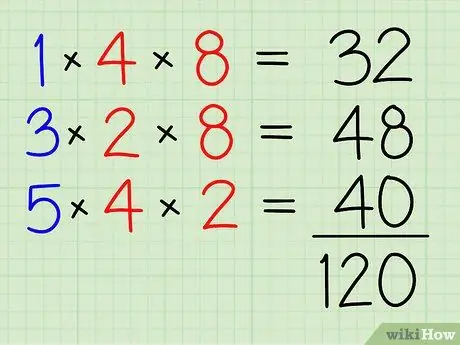
Trinn 4. Legg dem alle sammen
32+48+40=120
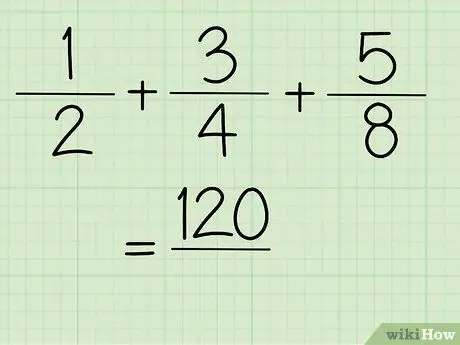
Trinn 5. Nå får du tellerverdien

Trinn 6. Løs nevneren til fraksjonen

Trinn 7. Multipliser alle brøkets nevnere
2×4×8=64

Trinn 8. Nå får du resultatet
120/64 = 1 56/64 = 1 ⅞
Advarsel
- Denne metoden lar deg multiplisere store tall.
- Du må kanskje ha en kalkulator for å beregne denne måten.






