- Forfatter Jason Gerald [email protected].
- Public 2023-12-16 11:30.
- Sist endret 2025-01-23 12:42.
Desimalsystemet (ti) har ti mulige verdier (0, 1, 2, 3, 4, 5, 6, 7, 8 eller 9) for hver tallposisjon. I kontrast har det binære (grunn to) tallsystemet bare to mulige verdier representert med 0 og 1 for hver tallposisjon. Siden det binære tallsystemet er det interne språket til elektroniske datamaskiner, vet seriøse dataprogrammerere hvordan de skal konvertere fra desimal til binært tallsystem. Følg disse enkle trinnene og også hvordan du mestrer denne konverteringen.
Steg
Metode 1 av 2: Short Division by Two med Rest

Trinn 1. Bestem problemet
For dette eksemplet, la oss konvertere desimaltallet 15610 være et binært tall. Skriv desimaltallet som tallet som skal deles i symbolet for invertert divisjon. Skriv basen til destinasjonsnummersystemet (i dette eksemplet "2" for binær) som den ut-av-kurve divisoren til divisjonssymbolet.
- Denne metoden er mye lettere å forstå når den er tegnet på papir, og mye lettere for nybegynnere, fordi den bare deler på to.
- For å unngå forvirring før og etter konvertering, skriv ned basenummeret til tallsystemet du beregner som et abonnement (små bokstaver skrevet med normale bokstaver som et kjennetegn) for hvert tall. I dette eksemplet vil desimaltallet ha et abonnement på 10 og det binære tallet vil ha et abonnement på 2.

Trinn 2. Gjør divisjonen
Skriv heltallssvaret (kvoten) under symbolet for lang divisjon, og skriv resten (0 eller 1) til høyre for det delte tallet.
Fordi vi deler med to, når tallet som deles er et partall, er resten 0, og når tallet som deles er et oddetall, er resten 1

Trinn 3. Fortsett å dele til det når null
Fortsett nedoverbakke, del hver ny kvotient med to og skriv resten til høyre for hvert delt nummer. Stopp når kvoten er null.

Trinn 4. Skriv ned det nye binære nummeret
Start fra det laveste gjenværende tallet, les rekkefølgen på resten i stigende rekkefølge til toppen. I dette eksemplet bør du få resultatet 10011100. Dette er den binære ekvivalenten til desimaltallet 156. Eller, hvis den er skrevet med den numeriske basen: 15610 = 100111002.
Denne metoden kan endres for å konvertere fra desimalbase til en hvilken som helst tallbase. Deleren er 2 fordi basen for destinasjonsnummersystemet er base 2 (binær). Hvis basen til destinasjonsnummersystemet er en annen base, må du erstatte basis 2 -nummeret i denne metoden med det riktige basenummeret. For eksempel, hvis destinasjonsbasen er base 9, erstatt base 2 -nummeret med 9. Det endelige resultatet vil være direkte i form av destinasjonsbasenummeret
Metode 2 av 2: Avledende kraft av to og subtraksjon

Trinn 1. Start med å lage et bord
Skriv ned kreftene til de to basenumrene i "tabell 2 -basen" fra høyre til venstre. Start kl 20, skriv det som "1". Øk rangen med 1 for hver rangering. Fullfør tabellen til du får et tall som er nærmest tallet på desimaltallsystemet du beregner. For dette eksemplet, la oss konvertere desimaltallet 15610 være et binært tall.

Trinn 2. Finn tallet med den største kraften til basenummer 2
Fra tabellen velger du det største tallet som er lik eller mindre enn tallet som skal konverteres. Tallet 128 er tallet med den største effekten av basenummer 2 og er også mindre enn 156, så skriv et tall "1" under denne boksen i tabellen, der det største tallet fra tabellen er til venstre (se tabell på bildet ovenfor). Trekk deretter 128 fra det opprinnelige tallet, får du: 156 - 128 = 28.
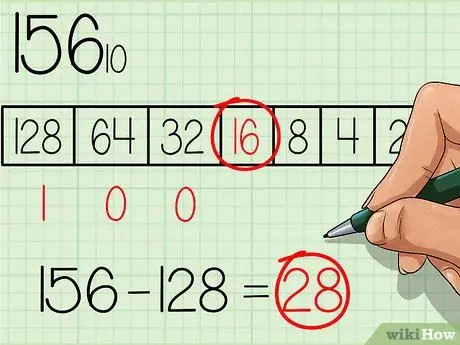
Trinn 3. Fortsett til neste mindre effekt i tabellen
Ved å bruke det nye nummeret (28), fortsetter du gjennom tabellen fra venstre til høyre mens du sjekker om tallene er lik eller mindre enn det nye tallet. Tallet 64 er ikke mindre enn 28, så skriv tallet “0” under tallboksen 64. Fortsett til du finner et tall som er lik eller mindre enn 28.
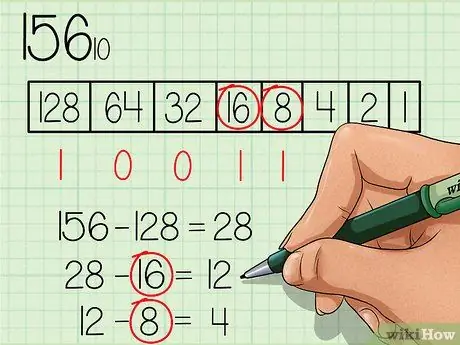
Trinn 4. Trekk fra hvert tall som er lik eller mindre enn det nye tallet kontinuerlig, og merk tallet "1" under boksen for det riktige tallet
Tallet 16 er mindre enn 28, så skriv tallet "1" under tallboksen 16 og trekk 16 fra 28, så får du et nytt tall 12. Tallet 8 er mindre enn 12, så skriv tallet "1" under tallboksen 8 og trekk 8 fra 12 for å få det nye tallet 4.

Trinn 5. Fortsett til du kommer til slutten av bordet
Husk å merke "1" under hver boks for tall som er lik eller mindre enn det nye tallet, og en "0" under hver boks for tall som fremdeles er større enn det nye tallet.
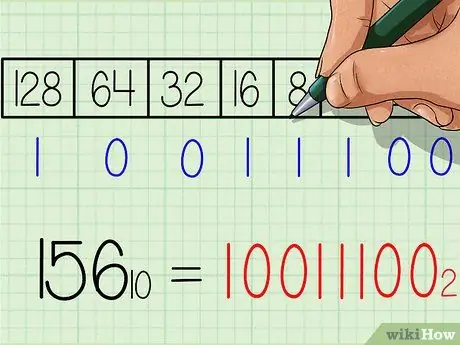
Trinn 6. Skriv ned svaret for det binære tallet
Tallet vil være nøyaktig det samme fra venstre til høyre som rekken med tall “1” og “0” nederst i tabellen. Du bør få resultatet 10011100. Dette er den binære ekvivalenten til desimalnummeret 156. Eller når det skrives med et abonnement: 15610 = 100111002.
Gjenta denne metoden kan hjelpe deg med å huske kreftene til grunn to, slik at du kan hoppe over trinn 1
Tips
- Kalkulatorprogrammet innebygd i operativsystemet kan gjøre denne konverteringen for deg, men som programmerer er det best å starte med en god forståelse av hvordan konverteringer fungerer. Konverteringsalternativene i kalkulatorprogrammet kan gjøres synlige ved å åpne "Vis" -menyen og velge "Programmerer" (for Windows 7 og 8).
- Konvertering i motsatt retning, dvs. fra det binære til desimaltallsystemet, er vanligvis lettere å lære først.
- Øv ofte på å konvertere desimaltall til binært for å bli mer ekspert.






