3 måter å finne gjensidighet eller gjensidighet

2024 Forfatter: Jason Gerald | [email protected]. Sist endret: 2024-01-15 08:21

Det gjensidige eller gjensidige er veldig nyttig i alle slags algebraiske ligninger. For eksempel, når du deler en brøk med en annen, multipliserer du den første fraksjonen med den gjensidige av den andre. Du må også bruke det inverse når du ser etter ligningen for en linje.

Steg

Metode 1 av 3: Finne det inverse av en brøk eller heltall

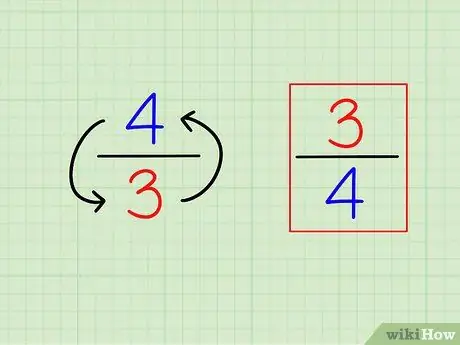
Trinn 1. Finn gjensidigheten til fraksjonen ved å snu den

Definisjonen av "gjensidig" eller det motsatte er veldig lett. For å finne det gjensidige av et helt tall, bare beregne "1 (det tallet)". For brøk er det gjensidige en annen brøk, det vil si at tallene er "inverterte" (inverse).

• For eksempel det motsatte av ³/₄ er ⁴/₃.
• Ethvert tall når det multipliseres med dets gjensidige avkastning 1.

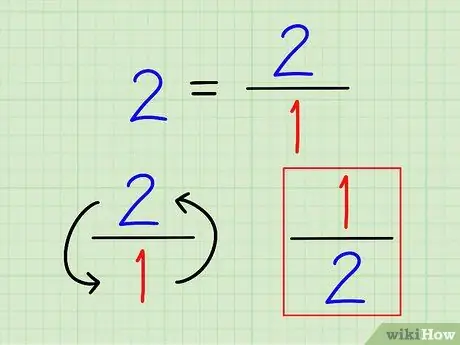
Trinn 2. Skriv det gjensidige av hele tallet som en brøk

Igjen er det gjensidige av et tall alltid 1 (det tallet). For hele tall, skriv dem som brøk. Det nytter ikke å beregne dette tallet til en desimal.

For eksempel er det gjensidige av 1 1 = ¹/₂.

Metode 2 av 3: Finne det inverse av en blandet brøk

Trinn 1. Identifiser blandede tall

Blandede brøker består av hele tall og brøk, for eksempel 2⁴/₅. Det er to trinn for å finne det gjensidige av et blandet tall som beskrevet nedenfor.

Trinn 2. Konverter blandede tall til feil brøk

Husk at 1 alltid kan skrives som (tall)/(samme tall), og brøk med samme nevner (bunnnummer) kan legges sammen. Her er et eksempel ved bruk av 2⁴/₅:

• 2⁴/₅
• = 1 + 1 + ⁴/₅
• = ⁵/₅ + ⁵/₅ + ⁴/₅
• = ^(5+5+4)/₅
• = ¹⁴/₅.

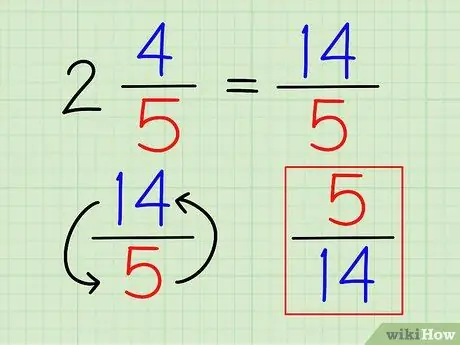
Trinn 3. Snu brøkdelen

Når tallet er skrevet helt som en brøkdel, kan du finne det gjensidige på samme måte som alle andre brøkdeler, ved å reversere brøken.

I eksemplet ovenfor er det gjensidige av ¹⁴/₅ er ⁵/₁₄.

Metode 3 av 3: Finne det motsatte av en desimal

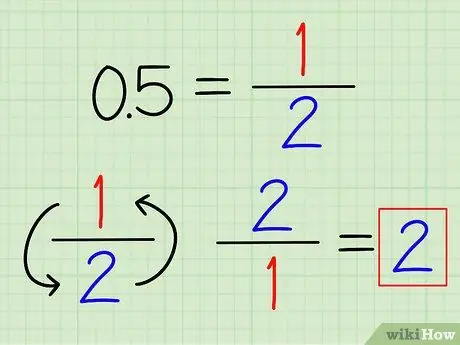
Trinn 1. Konverter desimaler til brøk hvis mulig

Du gjenkjenner kanskje noen ofte brukte desimaltall, som enkelt kan konverteres til brøk. For eksempel 0,5 = ¹/₂ og 0,25 = ¹/₄. Når desimalen er konvertert til en brøk, snu bare brøkdelen for å finne den gjensidige.

For eksempel er det gjensidige på 0,5 ²/₁ = 2.

Trinn 2. Skriv et delingsproblem

Hvis du ikke kan konvertere det til en brøkdel, beregner du gjensidigheten til tallet i form av et delingsproblem: 1 (desimal). Du kan bruke en kalkulator til å løse den, eller gå videre til neste trinn for å løse den manuelt.

For eksempel kan du finne gjensidig 0,4 ved å beregne 1 0,4

Trinn 3. Endre delingsproblemet for å bruke hele tall

Det første trinnet for å dele desimaler er å flytte desimaltegnet til alle tallene er hele tall. Så lenge du flytter desimalpunktet til begge tallene med samme antall trinn, får du det riktige svaret.

For eksempel kan du bruke 1 0, 4 og skrive det om til 10 4. I dette tilfellet flytter du alle desimalene ett trinn til høyre, på samme måte som du ganger hvert tall med ti

Trinn 4. Løs problemet ved å bruke lang divisjon

Bruk metoden for lang deling for å beregne det gjensidige. Hvis du teller 10 4, får du svaret 2, 5 som er det gjensidige av 0, 4.

Tips

• Den negative gjensidige av et tall er det samme som det vanlige gjensidige, ved at det multipliseres med det negative. For eksempel den negative gjensidige av ³/₄ er -⁴/₃.
• Det gjensidige eller gjensidige blir ofte referert til som "multiplikasjonsinversen".
• Tallet 1 er det motsatte av seg selv fordi 1 1 = 1.
• Tallet 0 har ingen gjensidig fordi 0 er udefinert.