- Forfatter Jason Gerald [email protected].
- Public 2024-02-01 14:14.
- Sist endret 2025-01-23 12:42.
Alt du trenger for å beregne gjennomsnittshastigheten er den totale forskyvningen. eller endring av posisjon, og total tid. Husk at hastighet også beregner retningen og hastigheten til et objekt, så inkluder en retning i svaret ditt, for eksempel "nord", "foran" eller "venstre". Hvis problemet med hastighetsberegning også innebærer konstant akselerasjon, kan du lære en rask måte å finne svaret på enda enklere.
Steg
Metode 1 av 2: Beregning av gjennomsnittlig hastighet på forskyvning og tid

Trinn 1. Husk at hastigheten inkluderer både hastigheten og retningen til et objekt
Velocity beskriver hastigheten som objektets posisjon endres med. Dette har ikke bare å gjøre med hvor raskt objektet beveger seg, men også med retningen. "100 meter per sekund sørover" er en annen hastighetsverdi enn "100 meter per sekund østover."
- Mengder som har retning kalles vektormengder '. Denne mengden kan skilles fra en retningsløs mengde som kalles en skalær mengde ved å skrive en pil over variabelen. For eksempel representerer notasjonen v frekvensen, mens notasjonen v → representerer hastighet eller hastighet + retning. V -notasjonen som brukes i denne artikkelen representerer hastighet.
- I vitenskapelige problemer bør du bruke målere eller andre metriske enheter for å uttrykke avstand, mens du til daglig bruk kan bruke hvilken som helst enhet du liker.
Trinn 2. Finn den totale fortrengningsverdien
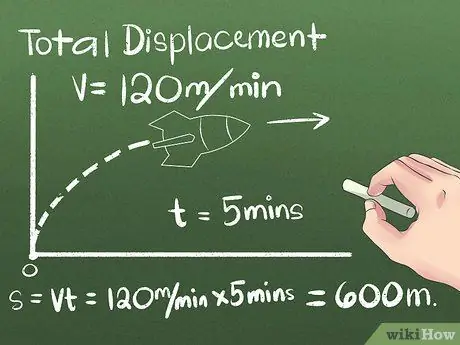
Forskyvning er endringen i et objekts posisjon, eller avstanden og retningen mellom start- og sluttpunktene. Retningen objektet beveger seg før den når sin endelige posisjon kan neglisjeres, fordi bare avstanden mellom start- og sluttpunktene blir tatt i betraktning. For det første eksemplet vil vi bruke et objekt som beveger seg med konstant hastighet i en retning:
- Si at en rakett beveger seg nordover i 5 minutter med en konstant hastighet på 120 meter i minuttet. For å beregne den endelige posisjonen, bruk formelen s = vt, eller bruk praktisk tenkning for å beregne avstanden som raketten reiste etter det (5 minutter) (120 meter/minutt) = 600 meter nord fra utgangspunktet.
- For problemer som involverer konstant akselerasjon, kan du løse dem med s = vt + at2, eller bruk den korte metoden beskrevet i en annen seksjon for å finne svaret.
Trinn 3. Finn den totale tiden du har brukt
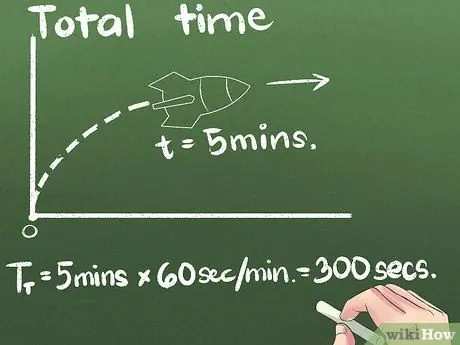
I vårt eksempel beveger raketten seg fremover i 5 minutter. Du kan uttrykke gjennomsnittshastigheten i en hvilken som helst tidsenhet, men den andre er den internasjonale vitenskapelige standardenheten. Vi vil endre enhetene i sekunder i dette eksemplet: (5 minutter) x (60 sekunder/minutt) = 300 sekunder.
Selv i vitenskapelige problemer, hvis spørsmålet bruker timen eller en større tidsenhet, vil det være lettere å beregne hastigheten først, og deretter konvertere det endelige svaret til meter/sekund
Trinn 4. Beregn gjennomsnittshastigheten som forskyvning over tid
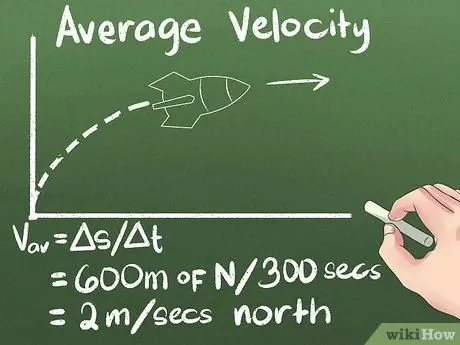
Hvis du vet hvor langt et objekt beveger seg, og hvor lang tid det vil ta å komme dit, vet du hvor fort det beveger seg. Så for eksempelet vi bruker, er gjennomsnittshastigheten til raketten (600 meter nord) / (300 sekunder) = 2 meter/sekund nord.
- Husk å inkludere en retning (for eksempel "foran" eller "nord").
- I formelen vav = s/Δt. Delta -symbolet betyr "endring", så s/Δt betyr "endring i posisjon over en periode".
- Gjennomsnittshastigheten kan skrives som vav, eller som en v med en horisontal linje over den.

Trinn 5. Løs mer kompliserte problemer
Ikke bli forvirret hvis et objekt endrer retning eller hastighet. Gjennomsnittshastigheten er fremdeles "bare" beregnet ut fra total forskyvning og total tid. Det som skjer mellom start- og sluttpunktene kan du ignorere. Følgende er noen eksempler på et objekt som reiser med samme forskyvning og total tid, og dermed samme gjennomsnittshastighet:
- Anna går vestover med 1 meter/s i 2 sekunder, så akselererer hun plutselig til 3 meter/sekund og fortsetter å gå vestover i 2 sekunder. Den totale forskyvningen er (1 m/s vestover) (2 sek) + (3 m/s vestover) (2 sek) = 8 meter vestover. Den totale tiden er 2 sekunder + 2 sekunder = 4 sekunder. Så gjennomsnittshastigheten er 8 meter vest/ 4 sekunder = 2 meter/andre vest.
-
Bart går vestover med 5 meter/sek i 3 sekunder, vender seg deretter om og går østover med 7 meter/sek i 1 sekund. Vi kan tenke på bevegelsen østover som "negativ vestlig bevegelse", så den totale forskyvningen er = (5 meter/sek vestover) (3 sek) + (-7 m/s vestover) (1 sek) = 8 meter. Total tid = 4 sekunder. Gjennomsnittlig hastighet = 8 meter vest / 4 sekunder = 2 meter/andre vest.
-
Charlotte gikk nord 1 meter og deretter gikk vest 8 meter, deretter sør 1 meter. Tiden det tar å fullføre hele reisen er 4 sekunder. Tegn diagrammet på et stykke papir, og du vil se sluttpunktet er 8 meter vest for startpunktet, så denne verdien er forskyvningen. Den totale tiden det tar er 4 sekunder, så gjennomsnittshastigheten er 8 meter vest / 4 sekunder = 2 meter/andre vest.
Metode 2 av 2: Beregning av gjennomsnittshastigheten for fast akselerasjon

Beregn gjennomsnittlig hastighet Trinn 6 Trinn 1. Vurder initialhastigheten og konstant akselerasjon
La oss si at problemet vårt er "En sykkel beveger seg til høyre med en hastighet på 5 m/s, med en konstant akselerasjon på 2 m/s2. Hvis denne sykkelen beveger seg i 5 sekunder, hva er gjennomsnittshastigheten?"
Hvis enheten "meter/sekund2"for å forvirre deg, skriv det som" meter/sekund/sekund "eller" meter per sekund per sekund. "En akselerasjon på 2 meter/sekund/sekund betyr at hastigheten øker med 2 meter per sekund hvert sekund.

Beregn gjennomsnittlig hastighet Trinn 7 Trinn 2. Bruk akselerasjon for å finne slutthastigheten
Akselerasjon, betegnet med notasjonen a, er hastigheten for hastighetsendring (eller hastighet). Hastigheten øker med en konstant økningshastighet. Du kan tegne et bord ved hjelp av akselerasjon for å finne hastigheten på forskjellige tidspunkter gjennom sykkelturen. Vi må lage denne tabellen for å finne sluttpunktet for problemet (ved t = 5 sekunder), men vi vil lage et lengre bord for å gjøre det lettere for deg å forstå dette konseptet:
- Ved startpunktet (tid t = 0 sekunder) beveger sykkelen seg med en hastighet på 5 meter/s.
- Etter 1 sekund (t = 1) beveger sykkelen seg med en hastighet på 5 meter/sekund + på = 5 meter/sekund + (2 meter/sekund2) (1 sekund) = 7 meter/sekund.
- Ved t = 2 beveger sykkelen seg til høyre med en hastighet på 5+ (2) (2) = 9 meter/sek.
- Ved t = 3 beveger sykkelen seg til høyre med en hastighet på 5+ (2) (3) = 11 meter/sek.
- Ved t = 4 beveger sykkelen seg til høyre med en hastighet på 5+ (2) (4) = 13 meter/sek.
- Ved t = 5 beveger sykkelen seg til høyre med en hastighet på 5+ (2) (5) = 15 meter/sekund.

Beregn gjennomsnittlig hastighet Trinn 8 Trinn 3. Bruk denne formelen for å finne gjennomsnittshastigheten
Hvis og "bare" hvis akselerasjonen er konstant, vil gjennomsnittshastigheten være lik gjennomsnittsverdien av summen av slutt- og starthastighetene. (vf +vJeg)/2. For vårt eksempelproblem ovenfor er sykkelens starthastighet vJeg 5 meter/sekund. Etter at vi har beregnet, er slutthastigheten vf 15 meter/sekund. Når vi legger disse to verdiene sammen, får vi (15 meter/sekund + 5 meter/sekund)/2 = (20 meter/sekund)/2 = 10 meter/sekund høyre retning.
- Husk å inkludere retningen, i dette tilfellet "riktig".
- Dette begrepet kan skrives som v0 (hastighet på tidspunkt 0, eller starthastighet) og v (slutthastighet).

Beregn gjennomsnittlig hastighet Trinn 9 Trinn 4. Forstå gjennomsnittshastighetsformelen intuitivt
For å finne gjennomsnittshastigheten kan vi bruke hastigheten når som helst og finne gjennomsnittet for dem alle. (Dette er definisjonen av et gjennomsnitt.) Siden dette krever beregning eller uendelig tid, må du forstå denne formelen mer intuitivt. I stedet for å ta hver gang, beregner du gjennomsnittshastigheten til de to tidspunktene og ser resultatene. Ett tidspunkt er nær starten av turen, hvor sykkelen går sakte, og et annet punkt er nær sluttpunktet hvor sykkelen går fort.

Beregn gjennomsnittlig hastighet Trinn 10 Trinn 5. Test intuitiv teori
Bruk tabellen ovenfor for å bestemme hastigheten på forskjellige tidspunkter. Noen par som oppfyller kriteriene våre er (t = 0, t = 5), (t = 1, t = 4) eller (t = 2, t = 3). Du kan teste denne formelen med andre t -verdier enn heltall, hvis du vil.
Uansett hvilket par du velger, vil gjennomsnittshastigheten på det tidspunktet alltid være den samme. For eksempel ((5+15)/2), ((7+13)/2) eller ((9+11)/2) er alle 10 meter/sek til høyre

Beregn gjennomsnittlig hastighet Trinn 11 Trinn 6. Fullfør den intuitive forklaringen
Hvis vi bruker denne metoden med en liste over hver gang vi tar den, fortsetter vi å beregne gjennomsnittet av første halvdel av turen og andre halvdel av turen. Tiden det tar å dekke hver halvdel er den samme, så ingen hastighet går tapt når vi er ferdige med å telle.
- Siden begge par vil gi samme resultat, vil gjennomsnittet av disse hastighetene også være det samme i verdi. I vårt eksempel er hastigheten til helheten "10 meter/sek til høyre" fremdeles på 10 meter/sek til høyre.
- Vi kan finne denne verdien ved å beregne gjennomsnittet av et hvilket som helst par, for eksempel start- og slutthastigheten. I vårt eksempel er disse hastighetene nådd ved t = 0 og t = 5, og kan beregnes ved hjelp av formelen ovenfor: (5+15)/2 = 10 meter/sek til høyre.

Beregn gjennomsnittlig hastighet Trinn 12 Trinn 7. Forstå denne formelen matematisk
Hvis du er mer komfortabel med bevis skrevet ned som formler, kan du starte med en formel for å beregne tilbakelagt distanse forutsatt konstant akselerasjon, og utlede formelen derfra:
- s = vJegt + kl2. (Teknisk s og t, eller endring i posisjon og endring i tid, men du ville også bli forstått hvis du skrev s og t.)
- Gjennomsnittlig hastighet vav definert som s/t, så skriv inn formelen i formen s/t.
- vav = s/t = vJeg + kl
- Akselerasjon x tid er lik endringen i total hastighet, eller vf - vJeg. Så vi kan erstatte "at" i formelen, og få:
- vav = vJeg + (vf - vJeg).
- Forenkle: vav = vJeg + vf - vJeg = vJeg + vf = (vf +vJeg)/2.
Tips
- Hastighet er forskjellig fra hastighet fordi hastighet er en vektormengde, mens hastighet er en skalær mengde. Vektormengder involverer både retning og størrelse, mens skalare mengder bare involverer størrelse.
- Hvis objektet beveger seg i en dimensjon, for eksempel venstre-høyre, kan du bruke et positivt tall for å representere en retning (for eksempel høyre) og et negativt tall for å representere en annen retning (venstre). Skriv denne notasjonen øverst på siden, slik at den er tydelig for folk som leser arbeidet ditt.






