- Forfatter Jason Gerald [email protected].
- Public 2023-12-16 11:30.
- Sist endret 2025-01-23 12:42.
Å legge til brøk er en veldig nyttig kunnskap. Denne ferdigheten er veldig lett å lære og bruke når du arbeider med matematiske problemer fra barneskolen til videregående. Denne artikkelen forklarer hvordan du legger til brøk, slik at du kan gjøre det på bare noen få minutter.
Steg
Metode 1 av 2: Legge til brøk med samme nevner

Trinn 1. Kontroller nevneren (tallet under kvotienten) for hver brøk
Hvis tallene er like, legger du til brøk med samme nevner. Hvis nevnerne er forskjellige, les den andre metoden.
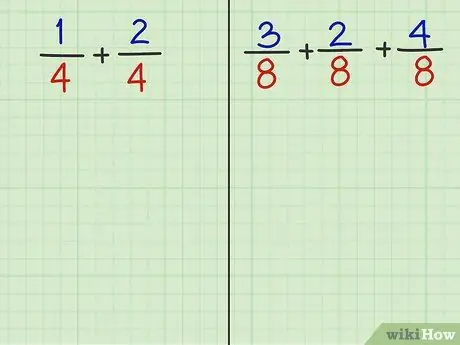
Trinn 2. Svar på følgende 2 spørsmål
Ved å lese det siste trinnet i denne metoden, bør du kunne legge sammen brøkene til de to følgende spørsmålene.
- Oppgave 1: 1/4 + 2/4
- Oppgave 2: 3/8 + 2/8 + 4/8
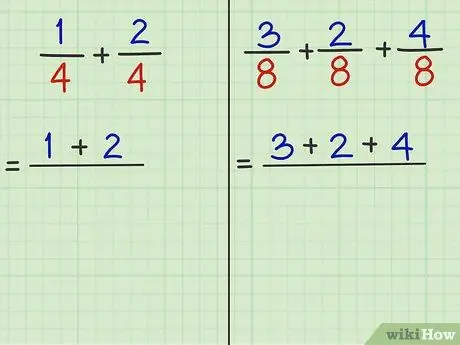
Trinn 3. Samle tellerne (tallene over skillet) og legg dem sammen
Telleren er tallet over kvotienten. Uansett hvor mange brøk du vil legge til, kan du legge til tellerne med en gang hvis nevnerne er de samme.
- Oppgave 1: 1/4 + 2/4 er brøkdelen som skal tilsettes. "1" og "2" er teller. Så 1 + 2 = 3.
- Oppgave 2: 3/8 + 2/8 + 4/8 er brøkdelen som skal legges til. "3" og "2" og "4" er teller. Så, 3 + 2 + 4 = 9.

Trinn 4. Bestem den nye brøkdelen fra summen
Skriv ned telleren som ble oppnådd i trinn 2. Dette tallet er ny teller. Skriv nevneren, som er det samme tallet under halvdelen av hver brøk. Du trenger ikke å gjøre beregningene hvis nevnerne er de samme. Dette tallet er ny nevner og er alltid lik den gamle nevneren når du legger til brøk med samme nevner.
- Oppgave 1: 3 er den nye telleren og 4 er den nye nevneren. Dermed er svaret på spørsmål 1 3/4. 1/4 + 2/4 = 3/4.
- Oppgave 2: 9 er den nye telleren og 8 er den nye nevneren. Dermed er svaret på spørsmål 2 9/8. 3/8 + 2/8 + 4/8 = 9/8.
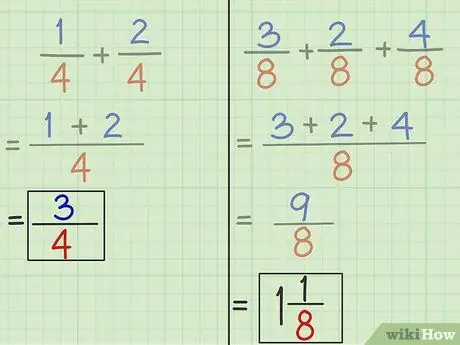
Trinn 5. Forenkle brøkene om nødvendig
Ikke glem å forenkle den nye brøkdelen for å gjøre skrivingen enklere.
-
Hvis telleren større i stedet for en nevner som resultatet av tillegg av problem 2, betyr dette at vi får 1 hel måned etter å ha forenklet brøken. Del telleren med nevneren eller 9 dividert med 8. Resultatet er et heltall 1 som er igjen 1. Skriv heltall foran brøkdelen og resten blir telleren til en ny brøk med samme nevner.
9/8 = 1 1/8.
Metode 2 av 2: Legge til brøk med forskjellige nevnere

Trinn 1. Kontroller nevneren (tallet under kvotienten) for hver brøk
Hvis nevnerne er forskjellige, er du det legge til brøk med forskjellige nevnere. Les trinnene nedenfor fordi du må gjøre nevnerne like før du legger til brøk.
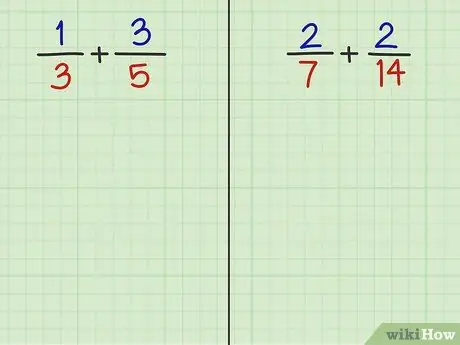
Trinn 2. Løs de følgende 2 spørsmålene
Ved å lese det siste trinnet i denne metoden, bør du kunne legge sammen brøkene til de to følgende spørsmålene.
- Oppgave 3: 1/3 + 3/5
- Spørsmål 4: 2/7 + 2/14

Trinn 3. Match nevnerne
For å gjøre dette, multipliserer nevnerne til de to brøkene ovenfor. En enkel måte å utligne nevnerne på er å multiplisere nevnerne til de to brøkene. Hvis en av nevnerne er et multiplum av den andre, finner du det minst felles multiplumet av de to nevnerne.
-
Oppgave 3:
3 x 5 = 15. Så den nye nevneren for begge brøkene er 15.
-
Oppgave 4:
14 er et multiplum av 7. Derfor trenger vi bare å multiplisere 7 med 2 for å få 14. Dermed er den nye nevneren for begge brøkene 14.

Trinn 4. Multipliser telleren og nevneren til den første fraksjonen med nevneren til den andre fraksjonen
Dette trinnet endrer ikke verdien av brøkdelen, men fraksjonen ser ut til å endre seg for å matche nevneren. Brøkverdien forblir den samme.
-
Oppgave 3:
1/3 x 5/5 = 5/15.
-
Oppgave 4:
For dette problemet trenger vi bare å multiplisere den første fraksjonen med 2/2 for å få nevnerne like.
2/7 x 2/2 = 4/14

Trinn 5. Multipliser telleren og nevneren til den andre fraksjonen med nevneren til den første fraksjonen
I likhet med trinnene ovenfor endrer vi ikke verdien av brøkdelen, men brøkdelen ser ut til å endre seg for å utligne nevneren. Brøkverdien forblir den samme.
-
Oppgave 3:
3/5 x 3/3 = 9/15.
-
Oppgave 4:
Vi trenger ikke å multiplisere den andre fraksjonen fordi nevnerne er de samme.

Trinn 6. Skriv de to nye brøkene i rekkefølge
På dette tidspunktet har vi ikke lagt de to brøkene sammen, selv om vi kan. I trinnet ovenfor multipliserte vi hver brøk med 1. Nå vil vi sørge for at brøkene vi vil legge til har samme nevner.
-
Oppgave 3:
i stedet for 1/3 + 3/5, blir brøkdelen 5/15 + 9/15
-
Oppgave 4:
I stedet for 2/7 + 2/14 blir brøkdelen 4/14 + 2/14

Trinn 7. Legg tellerne til de to brøkene sammen
Telleren er tallet over kvotienten.
-
Oppgave 3:
5 + 9 = 14. 14 er den nye telleren.
-
Oppgave 4:
4 + 2 = 6. 6 er den nye telleren.

Trinn 8. Skriv fellesnevner (i trinn 2) under den nye telleren eller bruk nevneren til brøken multiplisert med 1 for å utligne nevneren
-
Oppgave 3:
15 er den nye nevneren.
-
Oppgave 4:
14 er den nye nevneren.

Trinn 9. Skriv en ny teller og en ny nevner
-
Oppgave 3:
14/15 er svaret 1/3 + 3/5 =?
-
Oppgave 4:
6/14 er svaret 2/7 + 2/14 =?

Trinn 10. Forenkle og redusere brøk
For å forenkle brøkdeler, teller og nevner med den største fellesfaktoren for de to tallene.
-
Oppgave 3:
14/15 kan ikke forenkles.
-
Oppgave 4:
6/14 kan reduseres til 3/7 etter å ha delt teller og nevner med 2 som den største fellesfaktoren 6 og 14.
Tips
- Kontroller at nevnerne er de samme før du legger til brøk.
- Ikke legg sammen nevnerne. Hvis nevnerne er like, bruk tallet som nevner etter at brøkene er lagt til.
- Hvis du vil legge til brøk med tall som består av hele tall og brøk, konverter disse tallene til brøk og legg dem opp i henhold til instruksjonene ovenfor.






