Så lenge du kjenner målet på de to andre vinklene, er det enkelt å finne den tredje vinkelen i en trekant. Du trenger bare å trekke summen av de to vinklene med 180 grader. Imidlertid er det også andre måter du kan bruke til å finne den tredje vinkelen på en trekant hvis formen på problemet er litt annerledes enn vanlig. Hvis du vil vite hvordan du finner den tredje vinkelen i en trekant, følger du guiden nedenfor.
Steg
Metode 1 av 3: Bruke tiltakene i de andre to vinklene
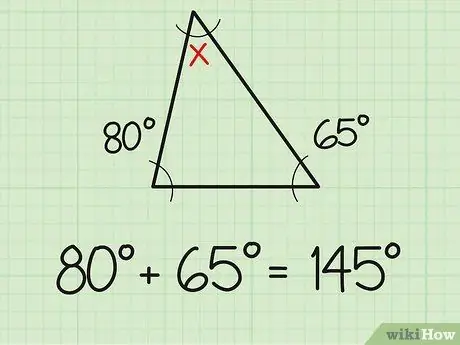
Trinn 1. Legg sammen de to kjente vinklene
Et faktum du bør vite er at summen av de tre vinklene i en trekant alltid er 180 grader. Så hvis du allerede kjenner målet på de to vinklene i en trekant, vil det å finne den tredje vinkelen være like enkelt som å gjøre enkle addisjons- og subtraksjonsproblemer. Legg først sammen de to vinkelmålene du allerede kjenner. For eksempel måler to kjente vinkler 80 og 65 grader. Legg de to sammen (80+65), så får du 145 grader.
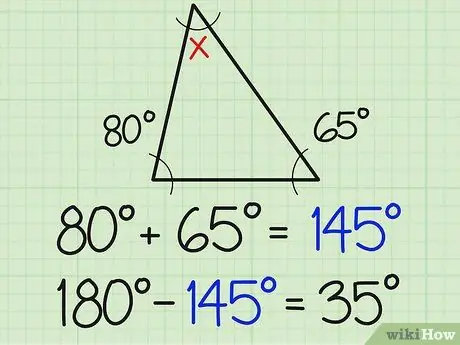
Trinn 2. Del dette tallet med 180
Summen av de tre vinklene i en trekant er alltid 180 grader. Derfor må den tredje vinkelen være 180 når den legges til summen av de to kjente målene for vinkelen. I eksemplet ovenfor betyr dette 180-154 = 35.
Trinn 3. Skriv svaret ditt
Nå har du svaret på den tredje vinkelen (i eksempelet 35 grader). Hvis du fortsatt er i tvil, se selv. Legg de tre vinklene sammen, så skal du få et resultat på 180. Hvis du ikke gjør det, er beregningen feil. For dette eksemplet, 80+65+35 = 180. Hvis det er riktig, betyr det at du har løst problemet.
Metode 2 av 3: Bruke variabler
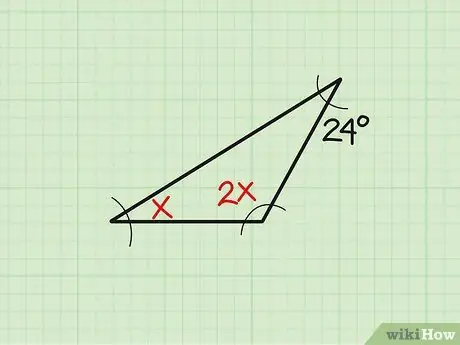
Trinn 1. Skriv ned problemet
Noen ganger vises størrelsen på den eksisterende vinkelen i en variabel form. La oss ta dette eksemplet: "Finn vinkelen" x "i en trekant hvis de tre vinklene måler henholdsvis" x "," 2x "og 24." Skriv først ned problemet.
Trinn 2. Legg sammen alle vinkelmålene
Prinsippet du må huske er det samme. Så, legg først sammen de tre vinklene i problemet, nemlig "x+2x+24 = 3x+24".
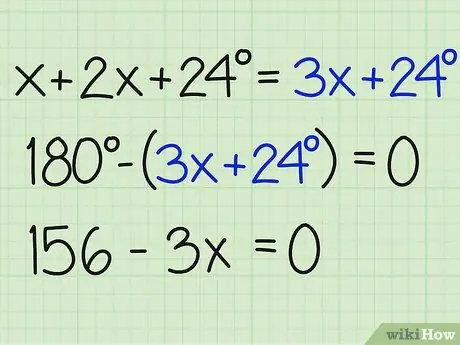
Trinn 3. Del summen av vinklene med 180
Forskjell dette tallet med 180 grader for å finne x og finne ut svaret på problemet. Sørg for at du avslutter ligningen lik null. Slik er det skrevet:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
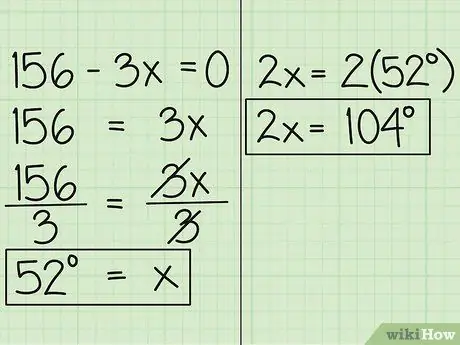
Trinn 4. Finn verdien av x
Flytt nå variabelen til den andre siden av ligningen, så får du 156 = 3x. Del deretter ligningen med 3, så får du x = 52. Dette betyr at målingen av vinkelen uttrykt i x er 52 grader. Den andre vinkelen, uttrykt i 2x er 52 grader ganger 2, som er 104 grader.
Trinn 5. Sjekk resultatene
Hvis du vil være sikker på at svaret ditt er riktig, legger du bare sammen de tre vinkelmålene du allerede har funnet svaret på. Hvis resultatet er 180, betyr det at svaret ditt er riktig. For dette eksempelet, 52+104+24 = 180.
Metode 3 av 3: Bruke andre metoder
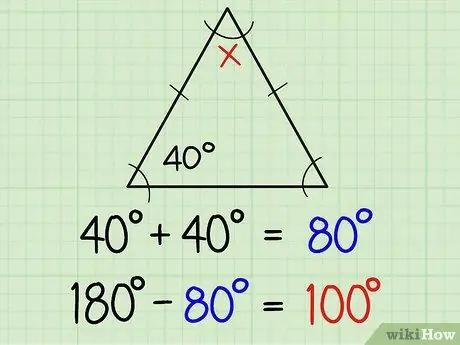
Trinn 1. Finn vinklene til en likebent trekant
En likebent trekant har to like sider og to like vinkler. To like sider er vanligvis merket med en liten linje midt på sidelinjen, noe som betyr at de to motsatte vinklene på linjen er samme mål. Hvis du allerede kjenner størrelsen på den ene vinkelen, kjenner du automatisk den andre vinkelen. Her er ytterligere forklaring:
Hvis en av de like vinklene er 40 grader, er den andre 40 grader. På den måten kan du finne alle tre vinklene med differansen mellom summen av 40+40 (dvs. 80) og 180, eller med andre ord 180-80 = 100
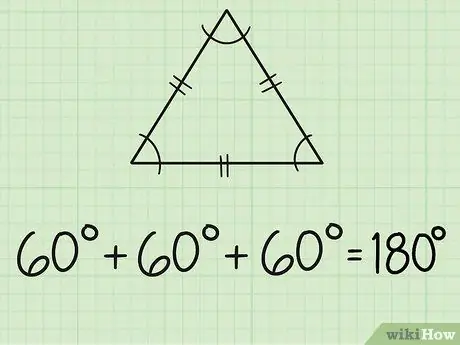
Trinn 2. Finn vinklene til en likesidet trekant
En likesidet trekant har tre like sider og tre like vinkler. Hver side er vanligvis merket med to korte linjer i midten. Siden alle tre vinklene er like, betyr det at alle vinklene måler 60 grader, fordi 180/3 = 60.
Trinn 3. Finn den tredje vinkelen i en rett trekant
Anta at du får en rett trekant, med en av spissvinklene som måler 30 grader. Siden trekanten er en rett vinkel, betyr det at en av vinklene, nemlig riktig vinkel, må måle 90 grader. Bruk deretter trekantprinsippet, differansen mellom summen av de to vinklene (90+30 = 120) med 180, så får du 180-120 = 60 grader.
