Det geometriske gjennomsnittet er en annen måte å finne gjennomsnittsverdien til et sett med tall, som gjøres ved å multiplisere verdiene før du tar røttene, i stedet for å legge sammen verdiene og dele dem som i et aritmetisk gjennomsnitt. Det geometriske gjennomsnittet kan brukes til å beregne gjennomsnittlig avkastning i finansiell analyse eller for å vise vekstraten til noe over en periode. For å finne det geometriske gjennomsnittet, multipliser alle verdiene før du roter med, som er det totale antallet tall i settet. Du kan også bruke logaritme -funksjonen i kalkulatoren til å finne det geometriske gjennomsnittet, hvis du foretrekker det.
Steg
Metode 1 av 2: Finne det geometriske gjennomsnittet av et sett med verdier
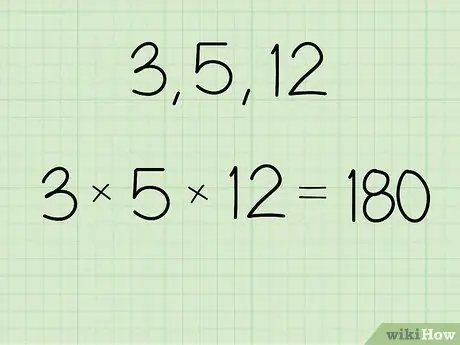
Trinn 1. Multipliser verdien du vil finne det geometriske gjennomsnittet for
Du kan bruke en kalkulator eller beregne manuelt for å få resultatet. Skriv ned resultatene, så du ikke glemmer det.
- For eksempel, hvis mengden tall er 3, 5 og 12, beregner du: (3 x 5 x 12) = 180.
- For et annet eksempel, hvis du vil finne det geometriske gjennomsnittet av settet med tall 2 og 18, skriver du: (2 x 18) = 36.
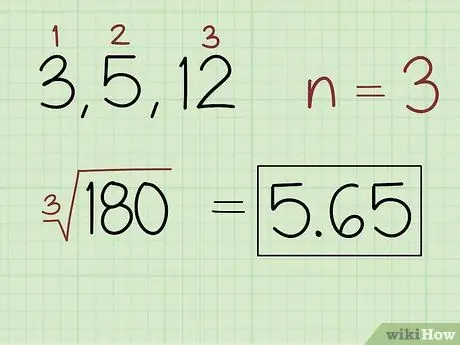
Trinn 2. Finn den niende roten til produktet, hvor n er antall verdier i settet
Telle antall tall i settet for å få verdien. Bruk verdiene til å angi roten som må brukes i produktet. Bruk for eksempel kvadratroten hvis settet inneholder 2 tall, kubikkrot hvis settet inneholder 3 tall, og så videre. Bruk en kalkulator for å løse ligningen og skrive ned svaret.
- For eksempel, for et sett med tall 3, 5 og 12, skriver du: (180) 5, 65.
- I det andre eksemplet med settet som inneholder 2 og 18, skriver du: (36) = 6.
Variasjon:
Du kan også skrive roten som eksponenten til 1/, hvis det er lettere å skrive på en kalkulator. For eksempel, for settet med tall 3, 5 og 12, skriver du (180)1/3 i stedet for (180).
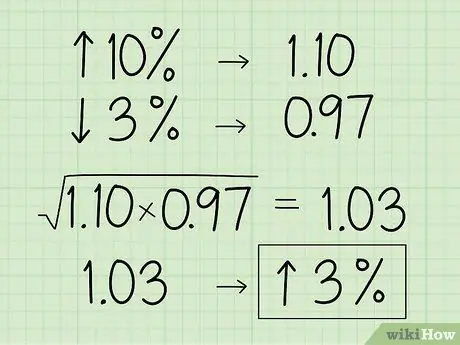
Trinn 3. Konverter prosentandelen til desimalmultiplikatorekvivalenten
Hvis mengden tall skrives som en økning eller reduksjon i prosent, prøv å ikke bruke prosentverdien i det geometriske gjennomsnittet fordi resultatene ikke vil være nøyaktige. Hvis prosentandelen øker, flytter du desimaltegnet to siffer til venstre og legger til 1. Hvis prosentandelen synker, flytter du desimalpunktet 2 siffer til venstre og trekker fra 1.
- For eksempel, si at du vil finne det geometriske gjennomsnittet av objektverdier som øker med 10%og deretter reduseres med 3%.
- Konverter 10% til et desimalnummer og legg til 1 for å få 1, 10.
- Konverter deretter 3% til et desimalnummer og trekk fra 1 for å få 0,97.
- Bruk begge desimalene for å finne det geometriske gjennomsnittet: (1, 10 x 0,97) 1,03.
- Konverter tallet tilbake til en prosentandel ved å flytte desimaltegnet med 2 siffer til høyre og trekke fra 1 for å få en verdiøkning på 3%.
Metode 2 av 2: Beregning av det geometriske gjennomsnittet ved hjelp av logaritmer
Trinn 1. Legg opp de logaritmiske verdiene for hvert tall i settet
LOG -funksjonen i kalkulatoren tar basen 10 av et tall og bestemmer hvor mye du trenger å multiplisere med 10 slik at det er lik tallet. Se etter LOG -funksjonen på kalkulatoren, som vanligvis er på venstre side av knappen. Klikk på LOGG -knappen og skriv inn det første nummeret i settet. Skriv "+" før du skriver inn LOG for det andre nummeret. Fortsett å skille LOG -funksjonen for hvert tall med et pluss -symbol før du får summen.
- For eksempel, for sett 7, 9 og 12, skriver du logg (7) + logg (9) + logg (12), og trykk deretter “=” på kalkulatoren. Hvis funksjonen er beregnet, vil tallet være rundt 2.878521796.
- Du kan også beregne hver logaritme separat før du legger dem sammen.
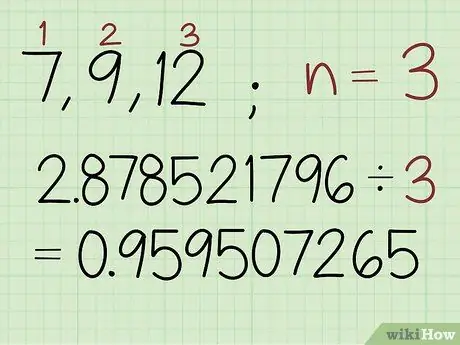
Trinn 2. Del summen av de logaritmiske verdiene med antall tall i settet
Tell antall verdier i settet og del det tidligere oppnådde tallet med det tallet. Resultatet er logaritmen til det geometriske gjennomsnittet.
I dette eksemplet er det 3 tall i settet, så skriv: 2, 878521796 /3 0, 959507265
Trinn 3. Finn antilog for kvoten for å bestemme det geometriske gjennomsnittet
Antilog -funksjonen er invers av LOG -funksjonen på kalkulatoren og konverterer verdien tilbake til base 10. Se etter symbolet “10x”På kalkulatoren, som vanligvis er en sekundær funksjon av LOG -knappen. Trykk på “2.” -knappen øverst i venstre hjørne av kalkulatoren etterfulgt av LOG -knappen for å aktivere antilog. Skriv inn kvoten som ble funnet i det siste trinnet før du løser ligningen.
I dette eksemplet viser kalkulatoren: 10(0, 959507265) ≈ 9, 11.
Tips
- Du kan ikke finne det geometriske gjennomsnittet av negative tall.
- Alle sett som har 0 vil ha et geometrisk gjennomsnitt på 0.
