IQR er interkvartilområdet eller kvartilrotområdet til et datasett. IQR brukes i statistisk analyse for å trekke konklusjoner om et datasett. IQR brukes oftere enn område fordi IQR ikke inkluderer de ytterste dataene. Fortsett å lese for å lære hvordan du finner IQR!
Steg
Metode 1 av 3: Forståelse av IQR
Trinn 1. Forstå hvordan du bruker IQR
I utgangspunktet er IQR en måte å forstå spredningen av et sett med tall. Rotkvartilområdet er definert som forskjellen mellom øvre kvartil (25% topp) og nedre kvartil (25% laveste) i datasettet.
Tips:
Den nedre kvartilen skrives vanligvis som Q1, og den øvre kvartilen skrives som Q3 - noe som teknisk gjør at midtpunktet til dataene er Q2 og det høyeste punktet til Q4.
Trinn 2. Forstå kvartilene
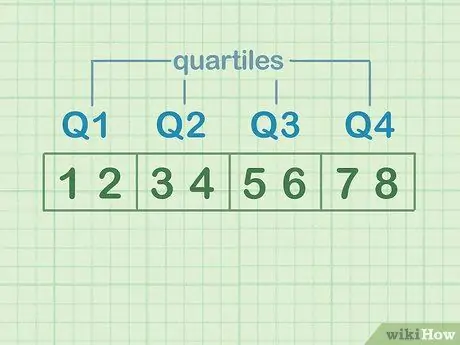
For å illustrere kvartiler, del mengden tall i fire like deler. Hver av disse delene er en "kvartil". Anta at datasettene er: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 og 2 er den første kvartilen eller Q1
- 3 og 4 er den andre kvartilen eller Q2
- 5 og 6 er den tredje kvartilen eller Q3
- 7 og 8 er fjerde kvartil eller Q4
Trinn 3. Lær formelen
For å finne forskjellen mellom de øvre og nedre kvartilene, må du trekke den 75. percentilen fra den 25. percentilen.
Formelen er skrevet: Q3 - Q1 = IQR
Metode 2 av 3: Kompilering av datasettet
Trinn 1. Samle inn dataene dine
Hvis du studerer IQR i klassen og i tester, kan du få et sett med data som allerede er forberedt, for eksempel 1, 4, 5, 7, 10. Dette er datasettet ditt - tallene du vil jobbe med. Imidlertid kan du bygge dine egne tall fra tabellspørsmål eller historieproblemer.
Sørg for at hvert tall representerer det samme:
for eksempel antall egg i hvert reir i en definert fuglebestand, eller antall parkeringsplasser i hvert hus i en spesifisert blokk.
Trinn 2. Sorter dataene i stigende rekkefølge
Med andre ord: ordne tallene fra minste til største. Bruk hintene fra eksemplene nedenfor.
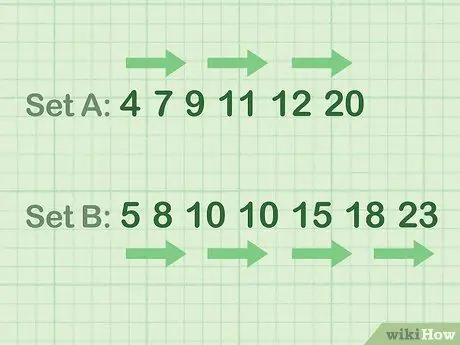
- Eksempel på partalldata (sett A): 4 7 9 11 12 20
- Eksempel på oddetalldata (sett B): 5 8 10 10 15 18 23
Trinn 3. Del dataene i to
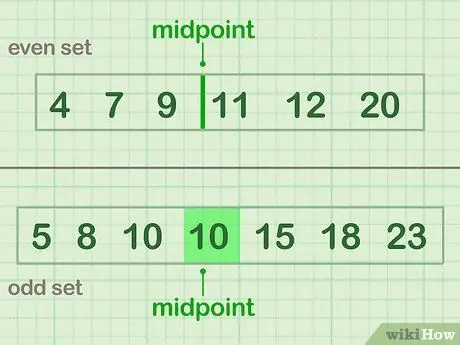
For å dele i to, finn midtpunktet for dataene dine: tallet eller tallene som er i sentrum av datasettet. Hvis du har et oddetall med data, velger du tallet som er midt i midten. Hvis du har et jevnt antall data, er midtpunktet mellom de to mest midtre tallene.
- Et jevnt eksempel (sett A) som har et midtpunkt mellom 9 og 11: 4 7 9 | 11 12 20
- Et merkelig eksempel (sett B) som har et midtpunkt av verdi (10): 5 8 10 (10) 15 18 23
Metode 3 av 3: Beregning av IQR
Trinn 1. Finn medianen for din nedre og øvre halvdel av dataene
Medianen er "midtpunktet" eller tallet som er midt i et sett med tall. I dette tilfellet ser du ikke etter midtpunktet for alle tallene, men leter etter det relative midtpunktet for de øvre og nedre dataundergruppene. Hvis du har et oddetall med data, må du ikke inkludere det midterste tallet - for eksempel i sett B trenger du ikke å inkludere et enkelt 10.
-
Selv eksempel (sett A):
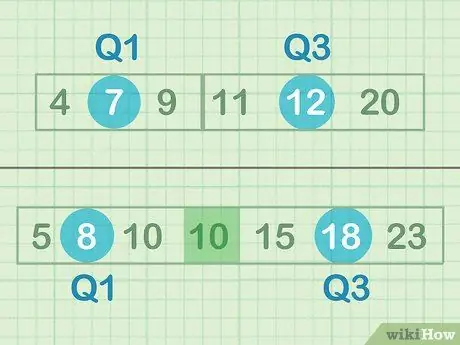
- Medianen for den nedre halvdelen av dataene = 7 (Q1)
- Medianen for den øvre halvdelen av dataene = 12 (Q3)
-
Merkelig eksempel (sett B):
- Medianen for den nedre halvdelen av dataene = 8 (Q1)
- Medianen for den øvre halvdelen av dataene = 18 (Q3)
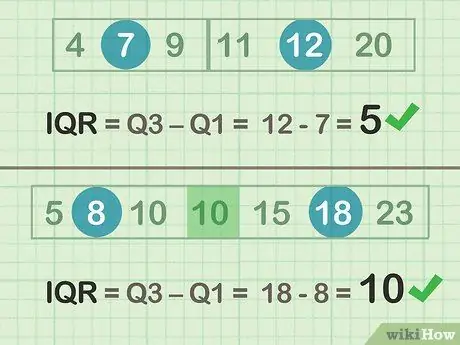
Trinn 2. Trekk fra Q3-Q1 for å bestemme IQR
Nå vet du hvor mange tall som faller mellom den 25. og 75. persentilen. Du kan bruke dette nummeret til å forstå spredningen av data. For eksempel, hvis en test har en maksimal score på 100, og IQR for poengsummen er 5, kan du anta at de fleste som tar testen har nesten samme forståelse fordi rekkevidden av høyder og nedturer ikke er veldig stor. Men hvis IQR for en testscore er 30, kan du begynne å lure på hvorfor noen scorer så høyt og andre scorer så lavt.
- Jevnt eksempel (sett A): 12 -7 = 5
- Merkelig eksempel (sett B): 18 - 8 = 10
Tips
Det er viktig å lære å gjøre dette på egen hånd. Det er imidlertid flere online IQR -kalkulatorer som du kan bruke til å kontrollere arbeidet ditt. Ikke stol for mye på kalkulator -apper hvis du lærer dette i timene! Hvis du blir bedt om å slå opp IQR i en test, må du vite hvordan du finner den manuelt
Relatert WikiHow
- Hvordan oppdage avvik
- Hvordan beregne rekkevidden til et datasett
- Hvordan lage en boks og teltdiagram
