- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:21.
- Sist endret 2025-01-23 12:42.
Tyngdekraften er en av de grunnleggende kreftene i fysikken. Det viktigste aspektet ved tyngdekraften er at det er universelt: alle objekter har en gravitasjonskraft som tiltrekker seg andre objekter. Gravitasjonskraftens størrelse avhenger av massen og avstanden mellom de to objektene.
Steg
Del 1 av 2: Beregning av tyngdekraften mellom to objekter

Trinn 1. Definer ligningen for gravitasjonskraften som trekker på et objekt, Fgrav = (Gm1m2)/d2.
For å kunne beregne gravitasjonskraften til et objekt, tar denne ligningen også hensyn til massene til de to objektene og deres avstand fra hverandre. Likningsvariablene er beskrevet nedenfor.
- Fgrav er tyngdekraften
- G er den universelle gravitasjonskonstanten 6.673 x 10-11 Nm2/kg2
- m1 er massen til det første objektet
- m2 er massen til det andre objektet
- d er avstanden mellom sentrene til de to objektene
- Noen ganger finner du bokstaven r i stedet for d. Disse to symbolene representerer avstanden mellom de to objektene.

Trinn 2. Bruk de aktuelle metriske enhetene
For denne ligningen må du bruke metriske enheter. Objektets masse må være i kilo (kg) og avstanden mellom objektene må være i meter (m). Du må konvertere disse enhetene til metriske enheter før du fortsetter

Trinn 3. Bestem massen til objektet det gjelder
For små gjenstander kan du veie dem for å bestemme vekten i kilo. For store gjenstander kan du slå opp den omtrentlige massen på et bord eller på internett. I fysikkproblemer vil vanligvis objektets masse bli fortalt.

Trinn 4. Mål avstanden mellom de to objektene
Hvis du prøver å beregne gravitasjonskraften mellom et objekt og jorden, må du vite hvor langt dette objektet er fra jordens sentrum.
- Avstanden fra jordoverflaten til sentrum av jorden er omtrent 6,38 x 106 m.
- Du kan slå opp tabeller eller andre kilder på internett som forteller deg den omtrentlige avstanden fra jordens sentrum til objekter i forskjellige høyder på jordoverflaten.

Trinn 5. Fullfør beregningen
Hvis du har definert variablene i ligningen, kan du skrive dem inn for å løse. Sørg for at alle variablene er i metriske enheter og at de er riktig skalert. Massen må være i kilo og avstanden må være i meter. Løs ligninger i riktig beregningsrekkefølge.
- For eksempel, bestem gravitasjonskraften til en person hvis masse er 68 kg over jordens overflate. Jordens masse er 5,98 x 1024 kg.
- Sørg for at alle variablene er i riktige enheter. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6.673 x 10-11 Nm2/kg2, og d = 6, 38 x 106 m
- Skriv ligningen din: Fgrav = (Gm1m2)/d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Multipliser massene av de to objektene som er tatt i betraktning. 68 x (5, 98 x 1024) = 4,06 x 1026
- Multipliser resultatet m1 og M2 med gravitasjonskonstanten G. (4,06 x 1026) x (6,67 x 10-11) = 2.708 x 1016
- Kvadrater avstanden mellom de to objektene. (6, 38 x 106)2 = 4,07 x 1013
- Delresultat G x m1 x m2 av avstanden i kvadrat for å oppnå gravitasjonskraften i Newton (N). 2, 708 x 1016/4, 07 x 1013 = 665 N
- Gravitasjonskraften er 665 N.
Del 2 av 2: Beregning av tyngdekraften på jorden

Trinn 1. Forstå Newtons andre lov, F = ma
Newtons andre lov sier at akselerasjonen til et objekt er direkte proporsjonal med nettokraften som virker på det og omvendt proporsjonal med massen. Med andre ord, hvis en kraft som virker på et objekt er større enn kraften som virker i motsatt retning, vil objektet bevege seg med den sterkere kraften.
- Denne loven kan oppsummeres med ligningen F = ma, hvor F er kraften, m er massen til objektet, og a er akselerasjonen.
- Takket være denne loven kan vi beregne gravitasjonskraften til alle objekter på jordoverflaten ved hjelp av den kjente akselerasjonen på grunn av tyngdekraften.
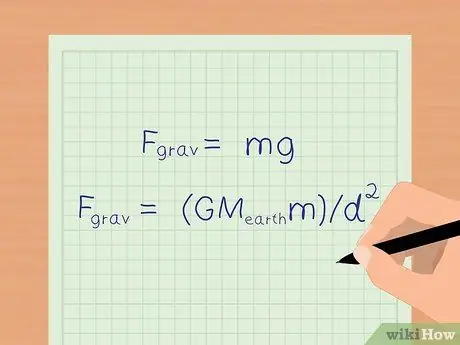
Trinn 2. Finn akselerasjonen på grunn av jordas tyngdekraft
På jorden får tyngdekraften alle objekter til å akselerere med 9,8 m/s2. På jordoverflaten kan vi bruke en forenklet ligning: Fgrav = mg for å beregne gravitasjonskraften.
Hvis du vil vite et mer presist antall gravitasjonskrefter, kan du fortsatt bruke formelen i forrige trinn, Fgrav = (GMJordm)/d2 for å bestemme gravitasjonskraften.

Trinn 3. Bruk de aktuelle metriske enhetene
For denne ligningen må du bruke metriske enheter. Objektets masse må være i kilo (kg) og avstanden mellom objektene må være i meter (m). Du må konvertere disse enhetene til metriske enheter før du fortsetter.

Trinn 4. Bestem massen til objektet det gjelder
For små gjenstander kan du veie dem for å bestemme vekten i kilo. For store gjenstander kan du slå opp den omtrentlige massen på et bord eller på internett. I fysikkproblemer vil vanligvis massen av objektet bli fortalt.

Trinn 5. Fullfør beregningen
Hvis du har definert variablene i ligningen, kan du skrive dem inn for å løse. Sørg for at alle variablene er i metriske enheter og at de er riktig skalert. Massen må være i kilo og avstanden må være i meter. Løs ligninger i riktig beregningsrekkefølge.
- La oss prøve å bruke ligningen i forrige trinn og se hvor nær resultatene er. Bestem gravitasjonskraften til en person med en masse på 68 kg på jordoverflaten.
- Sørg for at alle variablene er i riktige enheter: m = 68 kg, g = 9,8 m/s2.
- Skriv ned formelen. Fgrav = mg = 68*9, 8 = 666 N.
- Ved å bruke formelen F = mg er gravitasjonskraften 666 N, mens resultatet fra formelen i forrige trinn er 665 N. Som du kan se, er de to resultatene nesten like.
Tips
- Disse to formlene skal gi det samme svaret, men den kortere og enklere formelen er lettere å bruke når man diskuterer objekter på overflaten av en planet.
- Bruk den første formelen hvis du ikke kjenner akselerasjonen på grunn av tyngdekraften på en planet, eller hvis du beregner gravitasjonskraften mellom to veldig store objekter, for eksempel månen eller planeter.






