- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:14.
- Sist endret 2025-01-23 12:42.
Alle kan lære matematikk enten de allerede er på et høyere trinn i skolen eller som bare vil finpusse det grunnleggende igjen. Etter å ha diskutert hvordan du kan bli god til å lære matematikk, vil denne artikkelen lære deg de grunnleggende matematiske fremskrittene og gi deg de grunnleggende elementene du trenger å lære i hver øvelse. Deretter vil denne artikkelen diskutere det grunnleggende for å lære regning, som vil hjelpe både barneskolebarn og alle som ønsker å lære det grunnleggende innen dette vitenskapsfeltet.
Steg
Del 1 av 6: Nøkler til å bli en god matematikkstudent

Trinn 1. Vises i klassen
Når du savner klassen, bør du lære konsepter fra klassekamerater eller fra læreboken din. Du får aldri en tekstoppsummering fra en venn så mye som du får fra læreren din.
- Kom til timen i tide. I stedet kommer litt tidlig og åpner notatboken på riktig sted, åpner læreboken og tar ut kalkulatoren din, slik at du er klar til å begynne når læreren din er klar til å undervise.
- Bare truant hvis du er syk. Hvis du virkelig savner timen, kan du be klassekameratene om å finne ut hva læreren snakket om og hvilke lekser som ble gitt.

Trinn 2. Arbeid med læreren din
Hvis læreren din jobber med et problem foran klassen, kan du jobbe med læreren ved å jobbe med problemet i notatblokken.
- Sørg for at notatene dine er klare og lette å lese. Ikke bare skrive spørsmål. Skriv også ned alt læreren sier som kan forbedre din forståelse av begrepene som blir forklart.
- Fullfør eksemplene på spørsmålene fra læreren din. Når læreren går rundt i klassen mens du jobber, svarer du på spørsmålene som stilles.
- Delta når læreren løser et problem. Ikke vent til læreren ringer deg. Tilby deg å svare når du vet svaret, og løft hånden for å stille et spørsmål hvis du er usikker på materialet som blir undervist.

Trinn 3. Gjør leksene dine samme dag som leksene dine gis
Hvis du gjør leksene dine samme dag, er konseptet fortsatt friskt i tankene dine. Noen ganger er det ikke mulig å fullføre leksene dine samme dag. Sørg for at leksene dine er ferdige før du går til timen.

Trinn 4. Arbeid utenfor timen hvis du trenger hjelp
Besøk læreren din i pauser eller i kontortiden.
- Hvis du har et mattesenter på skolen din, kan du finne ut åpningstidene og be om hjelp.
- Bli med i en studiegruppe. En god studiegruppe består vanligvis av 4 eller 5 personer med forskjellige evner. Hvis du er en "C" -student i matematikk, kan du bli med i en gruppe på 2 eller 3 studenter med karakterer "A" eller "B", slik at du kan forbedre ferdighetene dine. Unngå å bli med i en gruppe studenter hvis karakterer er lavere enn dine.
Del 2 av 6: Lære matematikk på skolen

Trinn 1. Start med regning
På de fleste skoler lærer elevene regning på barneskolen. Aritmetikk dekker det grunnleggende om addisjon, subtraksjon, multiplikasjon og divisjon.
- Gjør øvelsesspørsmål. Å gjøre regningsproblemer om og om igjen er den beste måten å huske det grunnleggende riktig. Se etter programvare som kan gi deg en rekke forskjellige matematiske problemer å jobbe med. Se også etter problemer med tidsrammer for å forbedre hastigheten.
- Du kan også finne regningsproblemer på nettet, og du kan laste ned regne -apper til din mobile enhet.

Trinn 2. Fortsett med pre-algebra
Denne øvelsen gir deg de grunnleggende elementene du trenger for å løse algebraproblemer senere.
- Lær om brøk og desimaler. Du lærer å legge til, trekke fra, multiplisere og dele brøk og desimaler. Når det gjelder brøker, vil du lære å trekke fraksjoner og oversette kombinerte tall. Når det gjelder desimaler, vil du forstå stedsverdier, og du vil kunne bruke desimaler i historieproblemer.
- Lær om forhold, proporsjoner og prosenter. Disse begrepene vil hjelpe deg å lære å gjøre sammenligninger.
- Introduser deg selv for grunnleggende geometri. Du lærer 3D -former og -konsepter. Du lærer også begreper som areal, omkrets, volum og overflateareal, samt informasjon om parallelle og vinkelrette linjer og vinkler.
- Forstå noen grunnleggende statistikk. I pre-algebra inkluderer introduksjonen til statistikk generelt grafikk som grafer, spredningsdiagrammer, stempelplottdiagrammer og histogrammer.
- Lær det grunnleggende om algebra. Dette inkluderer begreper som å løse enkle ligninger som inneholder variabler, lære om egenskaper som den fordelende egenskapen, tegne enkle ligninger og løse ulikheter.
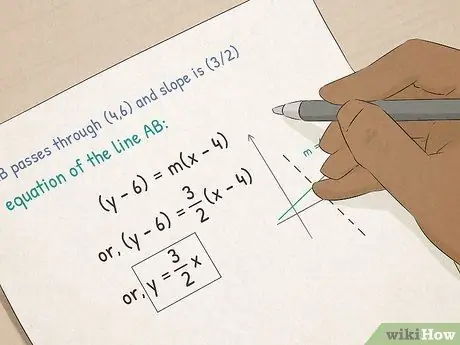
Trinn 3. Avansere til Algebra I
I ditt første år med algebra lærer du om de grunnleggende symbolene som er inkludert i algebra. Du vil også lære å:
- Løs ligninger og ulikheter som inneholder variabler. Du lærer hvordan du løser disse problemene på papir og hvordan du løser dem med bilder.
- Løs historieproblemer. Du vil bli overrasket over hvor mange dagligdagse problemer du vil møte i fremtiden som krever evnen til å løse algebraiske historieproblemer. For eksempel vil du bruke algebra for å finne ut renten du tjener på bankkontoen din eller investeringen. Du kan også bruke algebra til å finne ut hvor lenge du skal reise basert på bilens hastighet.
- Arbeid med eksponenter. Når du begynner å løse polynomligninger (uttrykk som inneholder tall og variabler), forstår du hvordan du bruker eksponenter. Dette vil trolig inneholde øvelser med vitenskapelig notasjon. Når du mestrer eksponenter, kan du lære å legge til, trekke fra, multiplisere og dele polynomuttrykk.
- Løs kvadrat- og kvadratrotproblemer. Når du mestrer dette emnet, vil du kunne huske kvadratene med mange tall. Du vil også kunne arbeide med ligninger som har kvadratrøtter.
- Forstå funksjoner og grafer. I algebra lærer du om grafiske ligninger. Du lærer hvordan du beregner skråningen på en linje, hvordan du setter en ligning i form-skråningsform, og hvordan du beregner x-og-y-delen av en linje ved hjelp av skjæringsskjæringsformen.
- Finn ut likningssystemet. Noen ganger får du 2 forskjellige ligninger med variablene x og y, og du må løse for x eller y for begge ligningene. Heldigvis lærer du mange triks for å løse disse ligningene, inkludert grafer, substitusjon og tillegg.

Trinn 4. Studer geometri
I geometri lærer du om egenskapene til linjer, segmenter, vinkler og former.
- Du vil huske en rekke teoremer og korollarier som vil hjelpe deg å forstå geometriens regler.
- Du lærer hvordan du beregner arealet til en sirkel, hvordan du bruker Pythagoras teorem og hvordan du finner forholdet mellom vinklene og sidene i en spesiell trekant.
- Du vil se mange geometri -spørsmål i fremtidige standardiserte tester som SAT, ACT og GRE.
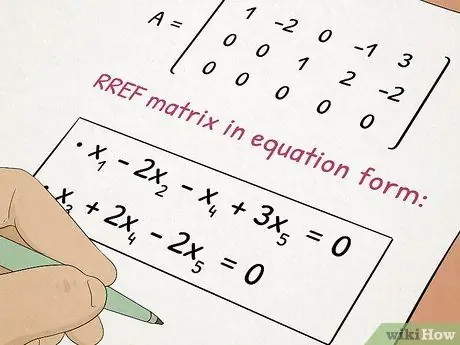
Trinn 5. Ta Algebra II -klassen
Algebra II bygger videre på begrepene du har lært i Algebra I mens du legger til komplekse emner som kvadratiske ligninger og matriser.
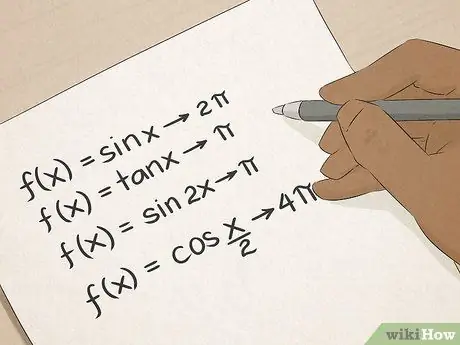
Trinn 6. Mestre trigonometri
Du kjenner trigonometriske termer: sinus, cosinus, tangens og så videre. Trigonometri vil lære deg mange praktiske måter å beregne vinkler og linjelengder på, og disse ferdighetene vil være uvurderlige for folk som jobber innen konstruksjon, arkitektur, ingeniørarbeid eller landmåling.
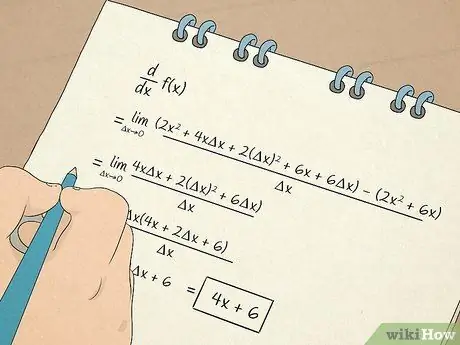
Trinn 7. Utfør beregningsberegninger
Calculus kan høres skremmende ut, men det er et fantastisk verktøy for å forstå enten oppførselen til tall eller verden rundt deg.
- Calculus vil lære deg funksjoner og grenser. Du vil se antall oppførsel av nyttige funksjoner, inkludert e^x og logaritmiske funksjoner.
- Du vil også lære å beregne og arbeide med derivater. Det første derivatet gir deg informasjon basert på skråningen til tangentlinjen til en ligning. For eksempel forteller et derivat deg hastigheten som noe endrer seg i en ikke-lineær situasjon. Det andre derivatet vil fortelle deg om funksjonen øker eller minker over et bestemt intervall, slik at du kan bestemme konkaviteten til en funksjon.
- Integraler vil lære deg hvordan du beregner arealet under en kurve, så vel som volumet.
- Regning på videregående skole ender vanligvis med sekvenser og sekvenser. Selv om studentene ikke vil se mange applikasjoner for kretser, er kretser viktige for de som studerer differensialligninger.
Del 3 av 6: Math Fundamentals-Master Addition

Trinn 1. Start med "+1" fakta
Hvis du legger 1 til et tall, kommer du til det høyeste tallet på tallinjen. For eksempel 2 + 1 = 3.
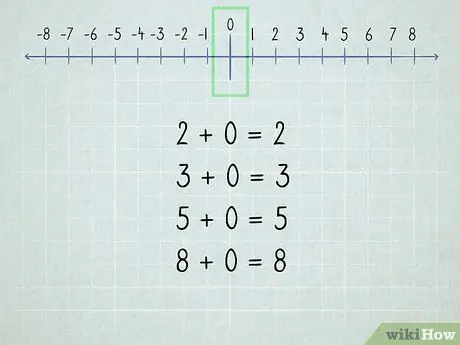
Trinn 2. Forstå nullpunktet
Alle tall lagt til null er det samme tallet fordi "null" betyr "ingen".

Trinn 3. Lær doble tall
Flere tall er et problem som innebærer å legge til to like tall. For eksempel er 3 + 3 = 6 et eksempel på en ligning som involverer flere tall.

Trinn 4. Bruk kartlegging for å lære om andre tilleggsløsninger
I eksemplet nedenfor lærer du ved å kartlegge hva som skjer når du legger til 3 til 5, 2 og 1. Prøv "legg til med 2" -problemet selv.

Trinn 5. Fortsett til tallet er mer enn 10
Lær å legge sammen 3 tall for å få et tall større enn 10.
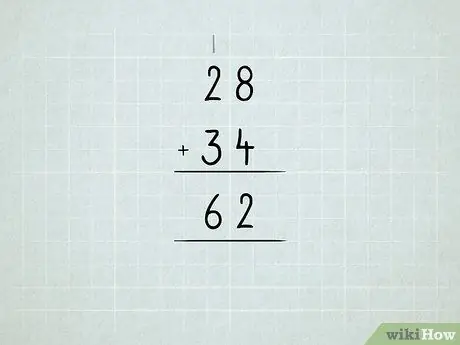
Trinn 6. Legg sammen de større tallene
Lær om å gruppere enheter i titalls, tiere i hundrevis, og så videre.
- Legg opp tallene i høyre kolonne først. 8 + 4 = 12, som betyr at du har 1 nummer 10 og 2 nummer 1. Skriv tallet 2 under kolonnen enheter.
-
Skriv tallet 1 i tienskolonnen.
-
Legg sammen tienskolonnen i sin helhet.
Del 4 av 6: Matematiske grunnleggende-reduksjonsstrategier

Trinn 1. Start med "bakover 1 siffer
Å trekke 1 fra et tall tar deg tilbake 1 tall. For eksempel 4 - 1 = 3.

Trinn 2. Lær å trekke fra doble tall
For eksempel legger du til tallene 5 + 5 for å få 10. Bare skriv ligningen bakover for å få 10 - 5 = 5.
- Hvis 5 + 5 = 10, så 10 - 5 = 5.
-
Hvis 2 + 2 = 4, så 4 - 2 = 2.

Trinn 3. Husk faktafamilien
Som et eksempel:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Trinn 4. Finn de manglende tallene
For eksempel, _ + 1 = 6 (svaret er 5).

Trinn 5. Husk faktum av subtraksjon til 20

Trinn 6. Øv på å trekke 1-sifrede tall fra 2-sifrede tall uten å låne
Trekk fra tallene i ene -kolonnen og reduser tallene i tienskolonnen.
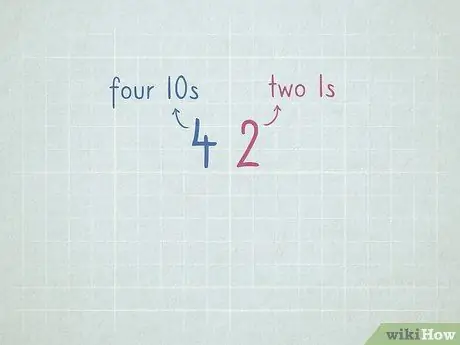
Trinn 7. Øv plassverdi for å forberede deg på å trekke fra ved å låne
- 32 = 3 tall 10 og 2 tall 1.
- 64 = 6 tall 10 og 4 tall 1.
- 96 = _ nummer 10 og _ nummer 1.
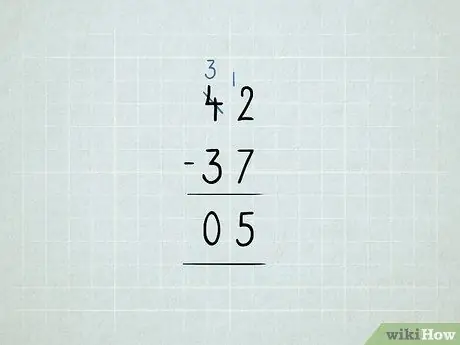
Trinn 8. Trekk fra ved å låne
- Du vil trekke fra 42 - 37. Du starter med å prøve å trekke fra 2 - 7 i enhetskolonnen. Det viste seg at det ikke fungerte!
-
Lån tallet 10 fra tienskolonnen og plasser den i kolonnen ener. Nå har du 3 10 -tallet i stedet for 4 -tallet. Nå har du 12 1 -tallet i stedet for 2 1 -tallet.
-
Trekk fra enhetens kolonne først: 12 - 7 = 5. Kontroller deretter kolonnen med tiere. Siden 3 - 3 = 0 trenger du ikke å skrive ned tallet 0. Svaret er 5.
Del 5 av 6: Math Fundamentals-Master Multiplication

Trinn 1. Start med tallet 1 og tallet 0
Alle tall som er ganget med 1 er det samme som selve tallet. Ethvert tall multiplisert med 0 er lik null.

Trinn 2. Lag multiplikasjonstabellen utenat

Trinn 3. Øv deg på ettsifrede multiplikasjonsproblemer

Trinn 4. Multipliser det tosifrede tallet med det 1-sifrede tallet
- Multipliser tallet nederst til høyre med tallet øverst til høyre.
-
Multipliser tallet nederst til høyre med tallet øverst til venstre.
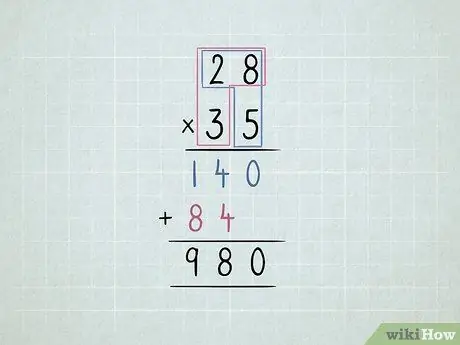
Trinn 5. Multipliser 2 2-sifrede tall
- Multipliser tallet nederst til høyre med nummeret øverst til høyre og deretter med nummeret øverst til venstre.
-
Flytt den andre raden ett siffer til venstre.
- Multipliser nummeret nederst til venstre med nummeret øverst til høyre og deretter tallet øverst til venstre.
-
Legg sammen alle kolonnene.
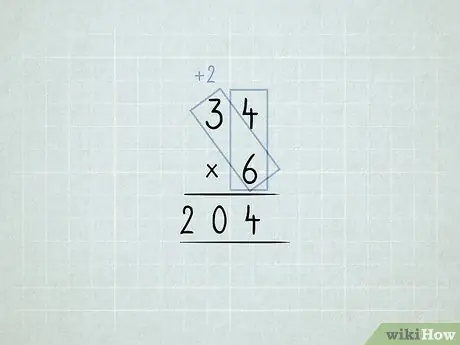
Trinn 6. Multipliser og grupper gruppene på nytt
- Du vil multiplisere 34 x 6. Du starter med å multiplisere enhetskolonnen (4 x 6), men du kan ikke ha 24 1s i en -kolonnen.
-
Lagre 4 1 -er i enhetskolonnen. Flytt 2 10s til tienskolonnen.
-
Multipliser 6 x 3, som tilsvarer 18. Legg til de 2 du flyttet, som tilsvarer 20.
Del 6 av 6: Matematiske grunnleggende-avslør delingsproblemer

Trinn 1. Tenk på divisjon i motsetning til multiplikasjon
#* Hvis 4 x 4 = 16, så 16 /4 = 4.
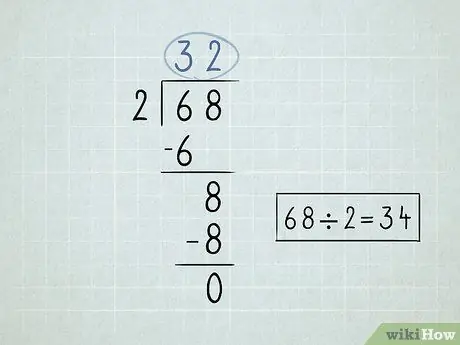
Trinn 2. Skriv ned delingsproblemet ditt
- Del tallet til venstre for divisjonssymbolet, eller divisor, med det første tallet under divisorsymbolet. Siden 6 /2 = 3, vil du skrive tallet 3 over divisjonssymbolet.
-
Multipliser tallet over divisjonssymbolet med divisoren. Ta resultatet ned til bunnen av det første tallet under divisjonssymbolet. Siden 3 x 2 = 6, vil du senke tallet 6 ned.
- Trekk fra de 2 tallene du har skrevet ned. 6 - 6 = 0. Du kan la 0 stå tomt, fordi du vanligvis ikke starter tall med 0.
-
Ta ned det andre tallet som er under divisjonssymbolet.
- Del tallet du kommer ned med divisoren. I dette tilfellet er 8 /2 = 4. Skriv tallet 4 over divisjonssymbolet.
-
Multipliser det øverste høyre tallet med divisoren og ta tallet ned. 4 x 2 = 8.
-
Trekk fra disse tallene. Den siste subtraksjonen returnerer null, noe som betyr at du har løst problemet. 68 x 2 = 34.

Trinn 3. Beregn også resten
Noen av delerne er ikke helt delt inn i andre tall. Hvis du har fullført den siste subtraksjonen, og du ikke har flere tall å hente, er det siste tallet resten.






