En matrise er et rektangulært arrangement av tall, symboler eller uttrykk i rader og kolonner. For å multiplisere en matrise må du multiplisere elementene (eller tallene) i første rad i matrisen med elementene i den andre raden i matrisen og legge sammen produktet. Du kan multiplisere matriser med bare noen få enkle trinn som krever riktig tillegg, multiplikasjon og plassering av resultatene.
Steg
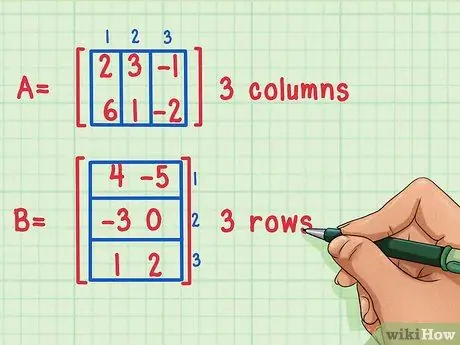
Trinn 1. Kontroller at matrisene kan multipliseres
Du kan bare multiplisere en matrise hvis antall kolonner i den første matrisen er lik antall rader i den andre matrisen.
Disse matrisene kan multipliseres fordi den første matrisen, Matrise A, har 3 kolonner, mens den andre matrisen, Matrise B, har 3 rader
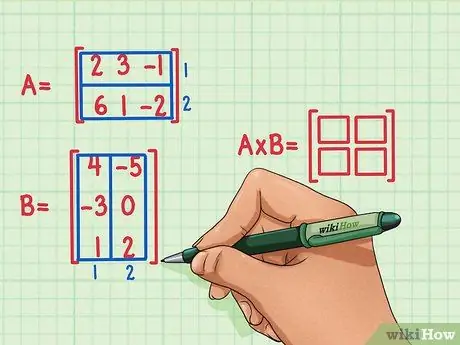
Trinn 2. Merk dimensjonene til matriseproduktet
Lag en ny, tom matrise, som vil markere dimensjonene til produktet til de to matrisene. Matrisen som representerer produktet av matrise A og matrise B vil ha samme antall rader som den første matrisen og samme antall kolonner som den andre matrisen. Du kan tegne tomme bokser for å vise antall rader og kolonner i denne matrisen.
- Matrise A har 2 rader, så resultatet av å multiplisere matrisen vil ha 2 rader.
- Matrise B har 2 kolonner, så resultatet av å multiplisere matrisen vil ha 2 kolonner.
- Resultatet av matriseproduktet vil ha 2 rader og 2 kolonner.
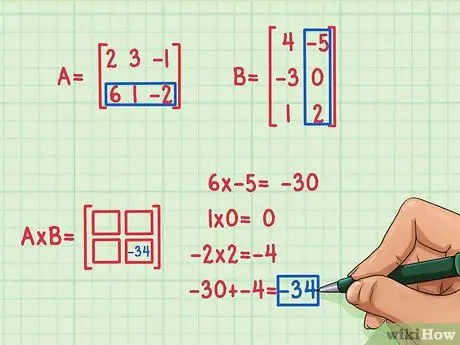
Trinn 3. Finn resultatet av det første prikkproduktet
For å finne resultatet av det første prikkproduktet, må du multiplisere det første elementet i den første raden med det første elementet i den første kolonnen, det andre elementet i den første raden med det andre elementet i den første kolonnen og det tredje elementet i den første raden ved det tredje elementet i den første kolonnen. Legg deretter til multiplikasjonsresultatene for å finne prikkprodukt (prikk).
Anta at du først har bestemt deg for å beregne elementene i andre rad og andre kolonne (nederst til høyre) i matriseproduktet. Slik gjør du det:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Resultatet av prikkproduktet er -34, og dette resultatet er skrevet nederst til høyre på matriseproduktet.
Når du multipliserer en matrise, blir prikkproduktet skrevet i radposisjonen til den første matrisen og kolonneposisjonen til den andre matrisen. For eksempel, når du kjenner prikkproduktet i den nederste raden i Matrise A og den høyre kolonnen i Matrise B, skrives svaret -34 i den nederste raden og høyre kolonne i matriseproduktet
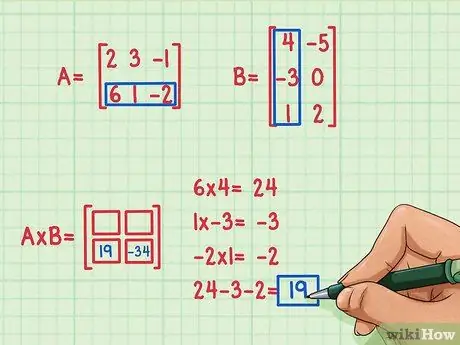
Trinn 4. Finn resultatet av det andre prikkproduktet
Anta at du vil finne begrepet nederst til venstre på matriseproduktet. For å finne dette begrepet trenger du bare å multiplisere elementene i den nederste raden i den første matrisen med elementene i den første kolonnen i den andre matrisen og deretter legge dem sammen. Bruk samme metode som å multiplisere første rad og kolonne - finn igjen prikkprodukt (gjør t)hans.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Resultatet av prikkproduktet er -19, og dette resultatet er skrevet nederst til venstre på matriksproduktet.
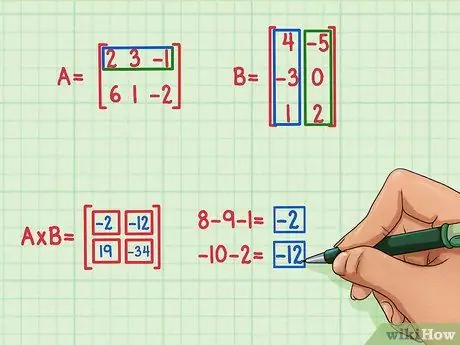
Trinn 5. Finn de to andre prikkproduktene
For å finne begrepet øverst til venstre i matriseproduktet, begynn med å finne prikkproduktet på den øverste raden i Matrise A og venstre kolonne i Matrise B. Slik gjør du det:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Resultatet av prikkproduktet er -2, og dette resultatet er skrevet øverst til venstre på matriksproduktet.
For å finne begrepet øverst til høyre i matriseproduktet, bare se etter prikkproduktet på den øverste raden i Matrise A og den høyre kolonnen i Matrise B. Slik gjør du det:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Punktproduktet er -12, og dette resultatet er skrevet øverst til høyre på matriseproduktet.
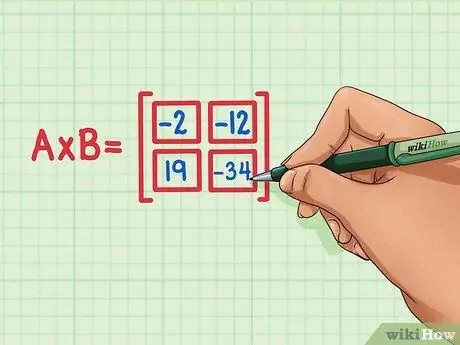
Trinn 6. Kontroller at de fire prikkproduktene er på riktig sted i matriseproduktet
19 må være nederst til venstre, -34 må være nede til høyre, -2 må være øverst til venstre, og -12 må være øverst til høyre.
Tips
- Å bruke linjesegmenter, og ikke bruke linjer, kan gi feil svar. Hvis en linje som representerer en rad krever en utvidelse for å krysse en kolonne, så forleng den! Dette er bare en visualiseringsteknikk for å gjøre det lettere for deg å vite hvilke rader og kolonner du skal bruke for å arbeide med hvert element i produktet.
- Produktet av de to matrisene vil produsere antall rader lik antall rader i den første matrisen og antall kolonner som er lik kolonnene i den andre matrisen.
- Skriv ned summen din. Å multiplisere matriser innebærer mange beregninger, og det er veldig enkelt å bli sidesporet og glemme hvilket tall du multipliserer.
