Det er lett å multiplisere brøker med blandede tall eller hele tall. Start med å konvertere blandede brøk eller hele tall til feil brøk (brøk med en større teller enn nevneren). Multipliser telleren av de to brøkene. Deretter multipliserer du de to nevnerne og forenkler produktet.
Steg
Metode 1 av 2: Multiplisere to blandede fraksjoner
Trinn 1. Konverter blandede fraksjoner til feil fraksjoner
For å konvertere et blandet tall, multipliserer nevneren med et eksisterende heltall. Deretter legger du til en teller i produktet. Plasser det endelige resultatet over linjen og ikke endre nevneren. Gjenta dette trinnet for de andre blandede fraksjonene.
For eksempel, hvis du har et 1 1/2 x 4 4/7 multiplikasjonsproblem, konverter begge brøkene til feil brøk. Brøk 1 1/2 kan endres til 3/2 og 4 4/7 endres til 32/7. Nå blir multiplikasjonsproblemet ditt 3/2 x 32/7
Trinn 2. Multipliser telleren for begge brøkene
Når du har to feil brøk og ikke flere heltall i problemet, multipliserer du de to tellerne. Skriv resultatet og plasser det over linjen.
- Telleren er alltid øverst i brøkdelen.
- For eksempel, for problemet 3/2 x 32/7, multipliser 3 med 32 for å få 96.
Trinn 3. Multipliser nevnerne for begge brøkene
Multipliser nå tallet under linjen og skriv resultatet under telleren.
For eksempel, for problemet 3/2 x 32/7, multipliser 2 med 7 for å få 14
Trinn 4. Konverter svar til blandede brøk hvis mulig
Hvis telleren til produktet er større enn nevneren, finner du et tall som produserer et tall som tilnærmet telleren når det multipliseres med nevneren (dette tallet vil fungere som et heltall senere). Deretter plasserer du differansen mellom produktet av nevneren med hele tallet og telleren over nevneren for å få formen for blandet tall.
- For eksempel, hvis du får 96/14 som et resultat av multiplikasjon, finner du tallet som resulterer i en sum som er nær 96 når det multipliseres med 14. Det tallet er 6, og du får 12 som differansen mellom 14 x 6 og 96. Plass 12 over nevneren (14).
- Vanligvis vil læreren be deg om å skrive svaret i samme form som spørsmålet. Hvis du får et blandet tall som et problem, må du også konvertere svaret til et blandet tall.
Trinn 5. Forenkle resultatene ytterligere hvis mulig
Det er mulig at du får både hele tall og brøk. Se på brøkene og sjekk om de kan forenkles. For eksempel, hvis du har et resultat på 6 12/14, del 12/14 med 2 for å forenkle det til 6/7.
I dette eksempelproblemet vil det endelige svaret være 6 6/7
Metode 2 av 2: Multipliser fraksjoner med heltall
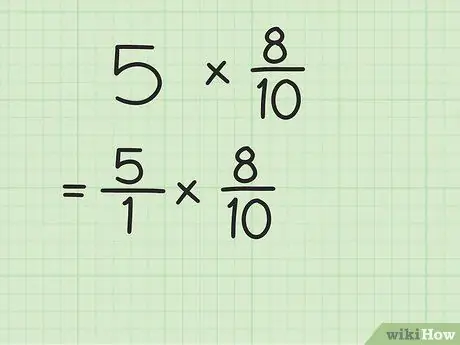
Trinn 1. Skriv om hele tallet som en brøk
For å omskrive et heltall som en brøk, plasserer du det ganske enkelt over tallet 1 (nevneren). Etter det vil de eksisterende heltallene bli til feil brøk.
For eksempel, hvis du har et problem på 5 x 8/10, plasser 5 over tallet 1. Nå er multiplikasjonen 5/1 x 8/10
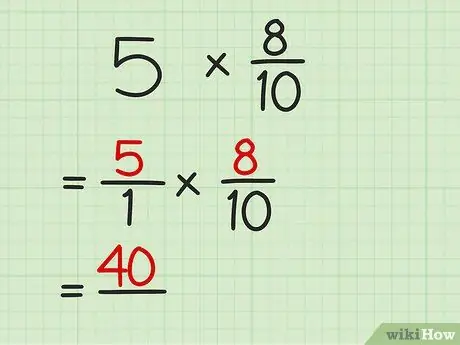
Trinn 2. Multipliser telleren for begge brøkene
Husk at telleren er tallet som er over linjen. Skriv ned resultatet og legg en linje under produktet.
For eksempel, i 5/1 x 8/10 problemet, multipliser 5 med 8 for å få 40
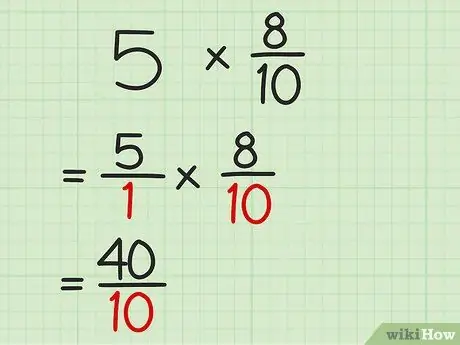
Trinn 3. Multipliser nevnerne for begge brøkene
På dette tidspunktet kan du multiplisere tallene under linjen for å få nevneren til produktet. Nå har du et multiplikasjonssvar i brøkform.
For eksempel, for et 5/1 x 8/10 problem, multipliser 1 med 10 for å få 10. Plasser tallet under linjen slik at produktet av de to brøkene er 40/10
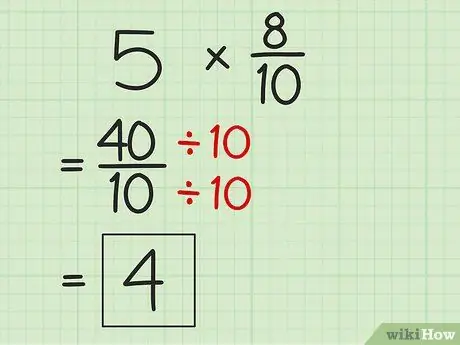
Trinn 4. Skjul svar hvis mulig
Siden produktet av produktet kan være en feilaktig brøkdel, forenkle resultatet til den minste formen. Del telleren med nevneren for å få et enklere resultat.
- For å forenkle 40/10, divider 40 med 10 for å få 4 som det nye svaret på multiplikasjonsproblemet.
- Vanligvis får du blandede tall fordi resultatet av divisjonen vil ha en rest.
