- Forfatter Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:49.
- Sist endret 2025-01-23 12:42.
Hastighet er en beregning av hvor fort noe beveger seg på en gang. Hvis du noen gang har sett på hastighetsmåleren til en bil i bevegelse, vil du se hastigheten telle - jo lenger nålen beveger seg, jo høyere hastighet er kjøretøyet. Det er flere måter å beregne hastighet på, avhengig av hvilken informasjon du har. Generelt formelen hastighet = distanse/tid (eller k = j/w) er den enkleste måten å beregne hastighet på.
Steg
Metode 1 av 3: Bruke standardhastighetsberegningsformler

Trinn 1. Finn avstanden et objekt har tilbakelagt
Den grunnleggende formelen som de fleste bruker for å finne hastigheten på noe er veldig enkel å bruke. Først av alt må du vite "hvor lang avstand har det målte objektet reist". Med andre ord, hva er avstanden mellom objektets startpunkt og sluttpunkt?
Denne formelen er lettere å forstå gjennom et eksempel. La oss si at vi reiser med bil til en lekeplass i "161 kilometer". I noen få trinn kan vi bruke denne informasjonen til å fullføre beregningen av formelen

Trinn 2. Finn tiden det tar objektet å reise den avstanden
Den neste informasjonen du trenger er hvor lang tid det tar objektet å nå en viss avstand. Med andre ord, hvor lang tid tar det før objektet beveger seg fra startpunktet til sluttpunktet?
I dette eksemplet, la oss si at objektet tar ca. to timer for å komme til destinasjonen.

Trinn 3. Del avstanden med tiden det tar å finne objektets hastighet
Du trenger bare disse to opplysningene for å kjenne objektets hastighet. Avstanden til tid er lik objektets hastighet.
I dette eksemplet er 161 kilometer/2 timer = 80,5 kilometer i timen.

Trinn 4. Ikke glem enheten som ble brukt
Det er veldig viktig å bruke riktige enheter i svaret ditt (for eksempel kilometer i timen, etc.) Uten disse enhetene er det veldig vanskelig for folk å forstå betydningen av svaret ditt. Du kan også miste poeng hvis du bruker feil enhet når du gjør oppgaver fra skolen.
Enheten for hastighet er avstandsenhet til tidsenhet. For eksempel, siden vi måler avstand i kilometer og tid i timer, er enhetene som brukes kilometer/time (eller kilometer i timen).
Metode 2 av 3: Løse vanskeligere beregninger

Trinn 1. Finn flere forskjellige variabler for å løse problemet med avstand og tid
Når du forstår den grunnleggende formelen for hastighet, kan du bruke den til å utføre andre beregninger enn hastighet. For eksempel, hvis du først bare kjenner hastigheten på objektet og en annen variabel, kan du omorganisere formelen ovenfor for å finne den ukjente informasjonen.
-
La oss for eksempel si at vi vet at et tog kjører i 20 kilometer i timen i fire timer, men vi vet ikke hvor langt det har reist. For å finne ut, kan vi omorganisere formelen på følgende måte:
-
- hastighet = distanse/tid
- hastighet × tid = (avstand/tid) × tid
- hastighet × tid = avstand
- 20 km/time × 4 timer = avstand = 80 kilometer
-

Trinn 2. Konverter enhetene du bruker etter behov
Noen ganger kan du beregne hastigheten ved å bruke en bestemt enhet, men du må konvertere den til en annen enhet. I dette tilfellet må du bruke en konverteringsfaktor for å få svaret i henhold til de riktige enhetene. For å gjøre dette, bare skriv forholdet mellom enhetene i brøkform og multipliser. Når du multipliserer, reverser brøkdelen etter behov for å fjerne uønskede enheter. Denne metoden er mye enklere enn den høres ut!
-
La oss for eksempel si at i eksempelproblemet ovenfor trenger vi svaret i miles i stedet for kilometer. En mil tilsvarer omtrent 1,6 kilometer. Så vi kan gjøre konverteringen som følger:
-
- 80 kilometer × 1,6 kilometer = 50 mil
-
- Husk at fordi kilometer vises nederst i brøkdelen, fjerner den kilometer fra forrige svar, så det endelige resultatet bruker miles.
- Dette nettstedet gir konverteringsfunksjoner for de fleste vanlige enheter.

Trinn 3. Erstatt variasjonen "avstand" med avstandsformelen etter behov
Objekter beveger seg ikke alltid i en rett, jevn bane. Hvis dette er sant, kan det hende du ikke bare kan angi en numerisk verdi som en enhet for avstand i standardhastighetsformelen. Imidlertid må du kanskje erstatte bokstaven j i formelen k = j/w med en formel som ligner distansen som objektet har tilbakelagt.
-
La oss for eksempel si at et fly roterer gjennom luften en avstand på 20 miles 5 ganger. Flyet fullførte runden på en halv time. I dette eksemplet må vi fremdeles finne den totale distansen som flyet med flyet før vi kan bestemme hastigheten. Vi kan bruke formelen for å beregne avstanden rundt en sirkel (avstand rundt den) i stedet for j i denne formelen. Denne formelen er omkrets = 2πr hvor r = sirkelradius. Slik løser du det:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 miles/time
-

Trinn 4. Forstå at k = j/w gir gjennomsnittshastigheten
Den enkle og enkle formelen vi bruker for å finne hastighet har en ulempe. Den resulterende verdien er teknisk gjennomsnittlig hastighet. Dette betyr at formelen antar at objektet du måler bruker samme hastighet som det beveger seg. Som vi vil se nedenfor, vil det være mye vanskeligere å finne hastigheten til et objekt i et enkelt øyeblikk.
For å illustrere denne forskjellen, tenk deg den siste gangen du reiste med bil. Det er usannsynlig at du reiser i samme hastighet som du reiser. Imidlertid vil du vanligvis starte reisen med lav hastighet og gradvis øke hastigheten underveis, stoppe på grunn av rødt lys, trafikkork, etc. Hvis du bruker standardhastighetsformelen for å finne hastighet under reise, kan endringer i den hastigheten ikke oppdages. Du vil imidlertid få et svar som viser gjennomsnittshastigheten til alle hastighetsforskjellene du reiser
Metode 3 av 3: Beregning av øyeblikkelig hastighet
Merk:
Denne delen bruker teknikker som er mindre kjent for folk som aldri har studert beregning. Les artiklene våre om beregning for å få hjelp.
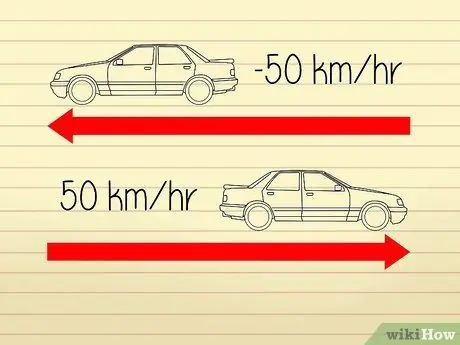
Trinn 1. Forstå at hastighet er definert som akselerasjonshastigheten
Høynivåberegninger er ganske forvirrende fordi matematikere og forskere bruker forskjellige definisjoner for å beskrive "hastighet" og "akselerasjon". Akselerasjon har to komponenter: en "hastighet" og en "retning". Hastigheten er lik objektets hastighet. En endring i retning vil føre til endring i akselerasjon, men ikke endring i hastighet.
- La oss for eksempel si at to biler beveger seg i motsatte retninger. Hastighetsmålere på begge bilene viser et tall på 50 km/t, så de kjører begge i samme hastighet. Siden bilene beveger seg bort fra hverandre, kan vi imidlertid si at den ene bilen har en "akselerasjon" på -50 km/t, mens den andre har en "akselerasjon" på 50 km/t.
- På samme måte som øyeblikkelige hastighetsberegninger, kan du også utføre øyeblikkelige akselerasjonsberegninger.

Trinn 2. Bruk absolutte verdier for å måle negativ akselerasjon
Et objekt kan ha en negativ akselerasjonshastighet (hvis det beveger seg i en negativ retning i forhold til et annet objekt). Det er imidlertid ingen negativ hastighet. Så i dette tilfellet indikerer den absolutte verdien av hastigheten objektets hastighet.
Av denne grunn, i eksempelproblemet ovenfor, har begge bilene en hastighet på 50 km/t.
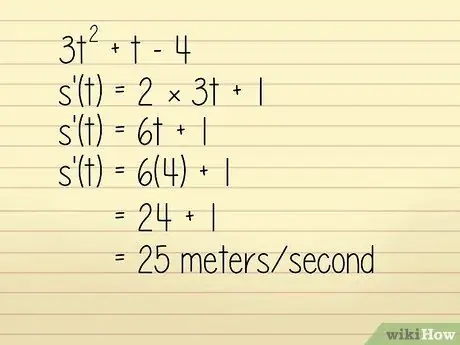
Trinn 3. Ta derivatet av posisjonen til funksjonen
Hvis du har en funksjon k (w) som viser posisjonen til et objekt uten å måtte beregne tiden, vil derivatet av k (w) vise akselerasjonen uten behov for timing. Bare koble tidsverdien til denne formelen slik at variabelen w (eller hvilken som helst tidsverdi som brukes) blir akselerert i henhold til den tiden. Herfra kan du enkelt finne objektets hastighet.
-
La oss for eksempel si at plasseringen av et objekt på en meter er beskrevet i ligningen 3q2 + w - 4 hvor w = tid i sekunder. Vi vil vite objektets hastighet ved w = 4 sekunder. I dette tilfellet kan du løse det ved å:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Nå skriver vi inn w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 meter/sekund. Teknisk er dette en beregning av akselerasjon, men siden den er positiv og retningen ikke er nevnt i spørsmålet, kan vi bruke den til å finne hastighet.
-

Trinn 4. Ta den integrerte akselerasjonsfunksjonen
Akselerasjon er en måte å måle endringen i akselerasjon av et objekt over tid. Dette emnet er for komplekst til å bli fullstendig forklart i denne artikkelen. Imidlertid er det nyttig å merke seg at når du har en funksjon a (w) som representerer akselerasjon med hensyn til tid, vil integralet av a (w) returnere resultatet av akselerasjon basert på den tiden. Husk at det er veldig nyttig å kjenne den første akselerasjonen til et objekt, slik at du kan definere konstanten til resultatet fra et uendelig integral.
-
La oss for eksempel si at et objekt har en konstant akselerasjon (i m/s2 som et resultat av a (w) = -30. Si også at objektet har en innledende akselerasjon på 10 m/s. Vi må finne hastigheten på w = 12 sekunder. I dette tilfellet kan vi løse det ved å:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
For å finne C, løser vi p (w) for w = 0. Husk at objektets første akselerasjon er 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, så p (w) = -30w + 10
-
-
Nå kan vi skrive inn w = 12 sekunder.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Siden hastighet er en absolutt verdi for akselerasjon, er objektets hastighet 350 meter/sekund.
-
Tips
- Øvelse gjør godt! Prøv å lage ditt eget spørsmål ved å erstatte tallene i eksempelproblemet ovenfor.
- Hvis du leter etter en rask måte å øve beregning for bedre beregningshastighet, kan du bruke den elektroniske derivatkalkulatoren her og den elektroniske integralkalkulatoren her.






